snypehype46
- 10
- 1
- Homework Statement
- Derive a similar equation for fermions
- Relevant Equations
- $$\psi(x) = \sum_s \int d\tilde{q} \left(a_s(q) u(q,s) e^{-iq \cdot x}+ b_s^\dagger(q) v(q,s) e^{iq \cdot x}\right)$$
I'm trying to the following exercise:

I've proven the first part and now I'm trying to do the same thing for fermions.
The formulas for the mode expansions are:
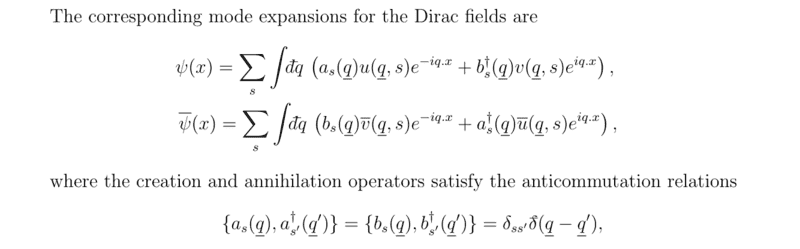
What I did was the following:
$$\begin{align*}
\sum_s \int d\tilde{q} \left(a_s(q) u(q,s) e^{-iq \cdot x}+ b_s^\dagger(q) v(q,s) e^{iq \cdot x}\right)|p,r\rangle = \\
\sum_s \int d\tilde{q} u(q,s) e^{-iq \cdot x} a_s(q) a^\dagger_r(p)|0\rangle +
\\ \sum_s \int d\tilde{q} v(q,s) e^{iq \cdot x} b_s^\dagger(q) b_r^\dagger(p) |0\rangle \\=
\sum_s \int d\tilde{q} u(q,s) e^{-iq \cdot x} \left( \delta_{rs} \delta(q-p) - a_r^\dagger(p)a_s(q)\right)|0\rangle + \\
\sum_s \int d\tilde{q} v(q,s) e^{iq \cdot x} b_s^\dagger(q) b_r^\dagger(p) |0\rangle
\end{align*}
$$
In the first the integral and the sum vanish because the kronecker delta and the delta function pick out a specific value of q and s.
Then taking multiplying from the left by ##\langle 0 |## we get:
$$u(p,s)e^{-ip\cdot x} \langle 0 | 0 \rangle + 0 = u(p,s)e^{-ip\cdot x}$$
where for the first term I've used the fact an annihilation operators gives zero acting on the vacuum and for the second term I've used the fact that:
$$\left(\langle 0 |b_s(q)\right)^\dagger = 0$$
Is this the correct way of proceeding? One thing I'm unsure is what I did for the writing of the state ##|p,r\rangle## is correct, because as you can see I "created" the state using two different operators in the same line: ##a_r^\dagger(p,r) |0 \rangle## and ##b_r^\dagger(p,r) |0 \rangle##.
I've proven the first part and now I'm trying to do the same thing for fermions.
The formulas for the mode expansions are:
What I did was the following:
$$\begin{align*}
\sum_s \int d\tilde{q} \left(a_s(q) u(q,s) e^{-iq \cdot x}+ b_s^\dagger(q) v(q,s) e^{iq \cdot x}\right)|p,r\rangle = \\
\sum_s \int d\tilde{q} u(q,s) e^{-iq \cdot x} a_s(q) a^\dagger_r(p)|0\rangle +
\\ \sum_s \int d\tilde{q} v(q,s) e^{iq \cdot x} b_s^\dagger(q) b_r^\dagger(p) |0\rangle \\=
\sum_s \int d\tilde{q} u(q,s) e^{-iq \cdot x} \left( \delta_{rs} \delta(q-p) - a_r^\dagger(p)a_s(q)\right)|0\rangle + \\
\sum_s \int d\tilde{q} v(q,s) e^{iq \cdot x} b_s^\dagger(q) b_r^\dagger(p) |0\rangle
\end{align*}
$$
In the first the integral and the sum vanish because the kronecker delta and the delta function pick out a specific value of q and s.
Then taking multiplying from the left by ##\langle 0 |## we get:
$$u(p,s)e^{-ip\cdot x} \langle 0 | 0 \rangle + 0 = u(p,s)e^{-ip\cdot x}$$
where for the first term I've used the fact an annihilation operators gives zero acting on the vacuum and for the second term I've used the fact that:
$$\left(\langle 0 |b_s(q)\right)^\dagger = 0$$
Is this the correct way of proceeding? One thing I'm unsure is what I did for the writing of the state ##|p,r\rangle## is correct, because as you can see I "created" the state using two different operators in the same line: ##a_r^\dagger(p,r) |0 \rangle## and ##b_r^\dagger(p,r) |0 \rangle##.