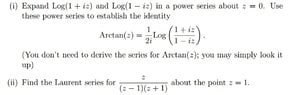- #1
nacho-man
- 171
- 0
Please refer to attached image.
Hi,
I'm a bit lost here with the first question. Unfortunately the online lecture covering this material isn't available due to their having been made some technical difficulties, and I find our textbook difficult to comprehend!
My lecture notes are pretty ambiguous in relation to these two questions.
Firstly, how exactly does one expand a log to a power series? Is there some trick required here, like converting the given logs to it's equivalent exponential, and then using the polar form?
Hi,
I'm a bit lost here with the first question. Unfortunately the online lecture covering this material isn't available due to their having been made some technical difficulties, and I find our textbook difficult to comprehend!
My lecture notes are pretty ambiguous in relation to these two questions.
Firstly, how exactly does one expand a log to a power series? Is there some trick required here, like converting the given logs to it's equivalent exponential, and then using the polar form?
Attachments
Last edited: