deuteron
- 64
- 14
- TL;DR Summary
- .
we know that we can expand the following function in Legendre polynomials in the following way
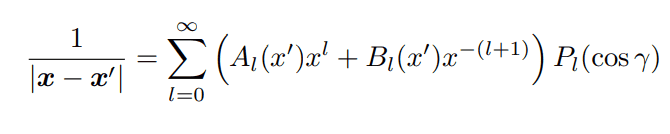
in the script given yo us by my professor, ##\frac 1 {|\vec x -\vec x'|}## is expanded using geometric series in the following way:
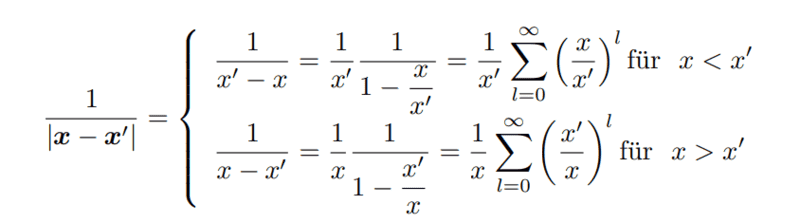
However, I don't understand how ##\frac 1 {|\vec x -\vec x'|}## is equal to both the above, and the below:
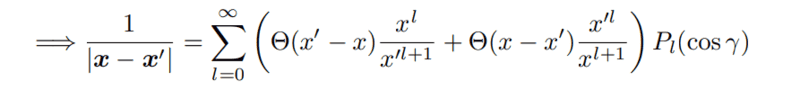
in the script given yo us by my professor, ##\frac 1 {|\vec x -\vec x'|}## is expanded using geometric series in the following way:
However, I don't understand how ##\frac 1 {|\vec x -\vec x'|}## is equal to both the above, and the below: