Expectation Maximization (EM) : find all parameters

[fab13]

I am tackling a technique to determine the parameters of a Moffat Point Spread Function (PSF) defined by:

$\text {PSF} (r, c) = \bigg (1 + \dfrac {r ^ 2 + c ^ 2} {\alpha ^ 2} \bigg) ^ {- \beta}$

with the parameter "(r, c) =" line, column "(not necessarily integers).

The observation of a star located at $(r_ {0}, c_ {0})$ with an amplitude $a$ and considering a background equal to $b$, can be modeled as:

$d (r, c) = a \cdot \text {PSF} _ {\alpha, \beta} (r-r_0, c-c_0) + b + \epsilon (r, c)$

with $\epsilon$ a centered Gaussian white noise.

Matrix notation can be used:

$d = H \cdot \theta + \epsilon$ with the parameter array $\theta = [a, b]$ and the followingmatrix $H$:

##$\begin{bmatrix}d(1,1) \\ d(1,2) \\ d(1,3) \\ \vdots \\ d(20,20) \end{bmatrix} = \begin{bmatrix} \text{PSF}_{\alpha,\beta}(1-r_0,1-c_0) & 1 \\ \text{PSF}_{\alpha,\beta}(1-r_0,2-c_0) & 1 \\ \text{PSF}_{\alpha,\beta}(1-r_0,3-c_0) & 1 \\ \vdots & \vdots \\ \text{PSF}_{\alpha,\beta}(20-r_0,20-c_0) & 1 \end{bmatrix} . \begin{bmatrix}a \\ b \end{bmatrix} + \begin{bmatrix}\epsilon(1,1) \\ \epsilon(1,2) \\ \epsilon(1,3) \\ \vdots \\ \epsilon(20,20) \end{bmatrix}$$the array$ \theta ## which is the array of parameters that we are trying to estimate.

1) In a first part of this exercise, the parameters $(\alpha, \beta)$ are fixed and one tries to estimate $\theta = [a, b]$, that is to say $a$ and $b$ by the likelihood method.

An estimator of the parameter array $\theta = [a, b]$ can be obtained directly by the following expression:

$\theta _ {\text {ML}} = \operatorname {argmin} _ {\theta} \sum_ {i = 1} ^ {N} \, (d(i) - (H \theta)(i)) ^ {2} = (H^T \, H)^{- 1} \, H^{T} \, d$

with $d$ the data generated with a standardized PSF (amplitude = 1).

**This technique works well to estimate $a$ and $b$ (relative to the fixed values).**2) Now, In the second part, I have to estimate $(a, b)$ but also $(r_ {0}, c_ {0}), \alpha, \beta$**, which means that I have to estimate the following array of parameters: $\nu = [r_ {0}, c_ {0}, \alpha, \beta]$ and I need to estimate this array $\nu$ at the same time as the parameters $\theta = [a b]$.

For this, we are first asked to put in matrix form this problem of estimation, according to $\nu$, $\theta$ and the matrix $H$.

But there, I wonder if I have just to use the same matricial form above ($\quad(1))$ ? such that :

$d = H \cdot \theta(\nu) + \epsilon \quad(1)$

So after, I would generate random values for $[r_{0}, c_{0}, \alpha, \beta]$ and $[a,b]$, wouldn't it ?

Below, an example of image from whch I have to estmate $\theta$ and $\nu$ parameters (20x20 dimensions) :

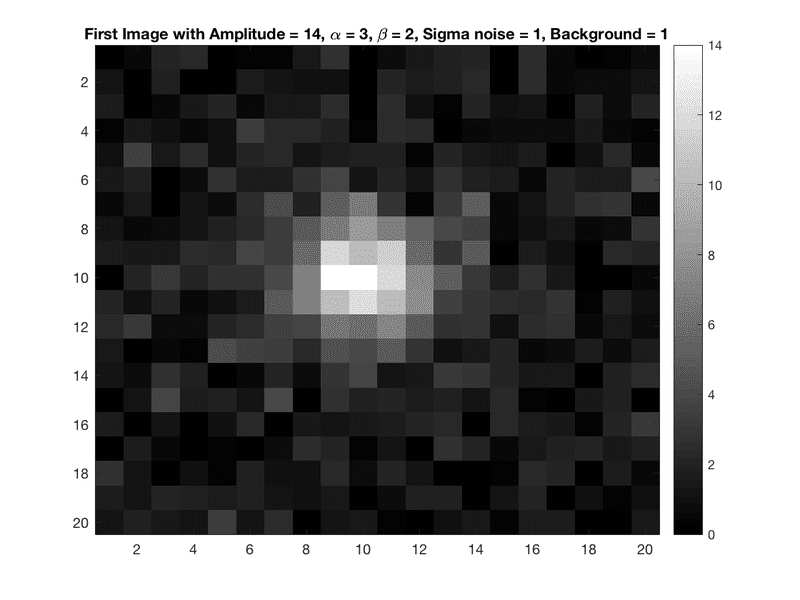
Just a last point, if anyone has the formula to apply to get directly an estimation of $\nu$ and $\theta$ parameters array (like for the first part where I used : $\theta_{\text{ML}} = (H^T \, H)^{- 1} \, H^{T} \, d$.

It seems, in this case, that I have to use a Cost function (to find the maximum or minimum : If someone could explain to me the principle of this cost function).

**UPDATE 1 :** From what I have seen, it seems the Expectation Maximization (EM) is appropriate for my problem.

The likelihood function is expressed as :

$\mathcal{L}=\prod_{i=1}^{n} \text{PSF}_{i}$

So I have to find $\nu$ and $\theta$ such that $\dfrac{\partial \text{ln}\mathcal{L}}{\partial \nu}=0$ and $\dfrac{\text{ln}\mathcal{L}}{\partial \theta}=0$

Could anyone help me to implement the EM algorithm to estimate $\nu$ and $\beta$ arrays of parameters ?

Regards

 

[mmwave]

Thank you for sharing your approach to estimating the parameters of the Moffat Point Spread Function. It seems like you have a good understanding of the problem and have already made progress in solving it.

To answer your question, yes, you can use the same matrix form as in (1) to estimate both the parameters $\theta$ and $\nu$. The only difference is that now your matrix $H$ will have more columns, as it will also include the parameters $r_0$ and $c_0$. So, the matrix form would look like:

$d = H \cdot \phi(\nu, \theta) + \epsilon \quad(2)$

where $\phi(\nu, \theta)$ is a function that combines both the parameters $\nu$ and $\theta$.

To generate random values for the parameters, you can use a similar method as in the first part of the exercise. However, keep in mind that now you have more parameters to estimate, so it might be helpful to have some initial guesses for the parameters to start with.

Regarding your question about the cost function, it is a function that measures how well your estimated parameters fit the observed data. In this case, it would be the sum of squared errors between the observed data and the data predicted by your model. The goal is to minimize this cost function to find the best estimates for your parameters.

As for implementing the EM algorithm, it might be helpful to break it down into smaller steps and familiarize yourself with the algorithm first. Once you have a good understanding of it, you can start implementing it in your code. Additionally, there are many resources available online that can help you with implementing the EM algorithm for your specific problem.

I hope this helps. Best of luck with your research.A fellow scientist