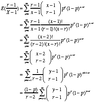Expected Value of Negative Binomial Random Variable

[pp123123]

Given $X$ as a negative binomial random variable with parameters $r$ and $p$.
Find $E(\frac{r-1}{X-1})$.

As $E(g(X))$ is defined as $\sum_{x\in X(\Omega)}g(x)p(x)$,

this is my attempt in which I am stuck.
View attachment 2115

What can I do next? In the case $y=r-1$, is the sum invalid?

Thanks in advance!

 

[Aaron Bex]

\begin{align*}
E\left(\frac{r-1}{X-1}\right)&=\sum_{x=0}^{\infty}\frac{r-1}{x-1} \binom{x-1+r-1}{x-1}p^r(1-p)^{x-1}\\
&=\sum_{x=0}^{\infty}\frac{r-1}{x-1} \binom{x+r-2}{x-1}p^r(1-p)^{x-1}\\
&=\sum_{x=1}^{\infty}\frac{r-1}{x-1} \binom{x+r-2}{x-1}p^r(1-p)^{x-1}\\
&=(r-1)\sum_{x=1}^{\infty}\binom{x+r-2}{x-1}p^r(1-p)^{x-1}\\
&=(r-1)\sum_{x=1}^{\infty}\frac{(x+r-2)!}{(x-1)!(r-2)!}p^r(1-p)^{x-1}\\
&=(r-1)\sum_{x=1}^{\infty