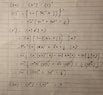Expected value of variance of Hamiltonian in coherent states

[graviton_10]

Homework Statement

Find the variance of the energy in coherent state |ɑ>.

Relevant Equations

<ΔH> = <ɑ| HH |ɑ>

I am trying to find the expected value of the variance of energy in coherent states. But since the lowering and raising operators are non-hermitian and non-commutative, I am not sure if I am doing it right. I'm pretty sure my <H>² calculation is right, but I'm not sure about <H²> calculation.

Here is my solution:

 

[TSny]

Check the step circled in orange. $a^\dagger$ and $a$ don't commute.

 

[graviton_10]

Yes, but how to do it the right way?

 

[TSny]

Yes, but how to do it the right way?

Please post the steps for how you reduced $\langle \alpha | (a^{\dagger} a)^2|\alpha \rangle$ to $|\alpha^*\alpha|^2 \langle \alpha | \alpha \rangle$. That way, we can help you see where you made a mistake.

 

[graviton_10]

So, I used the fact that the commutator of a and a dagger is 1. Does it look good now?

 

[TSny]

That looks good.