Experimentally calculating the acceleration due to gravity

[acertainayush]

[Mentors' note: No template because the thread was moved from the technical forums]

TL;DR Summary: I need help with determining the value of 'g' using the data I have collected in the lab, using an apparatus consisting of light gates fixated on a stand, the positions of which can be varied.

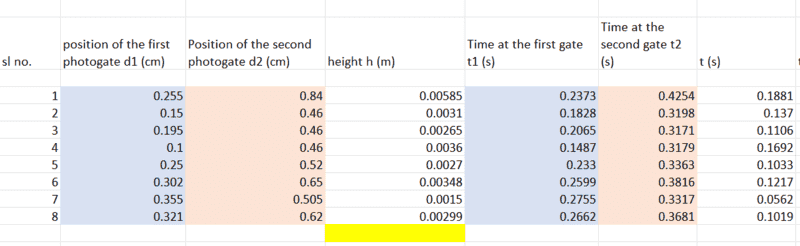
I have attached what my apparatus looked like, and my analysis. A metal ball is held at an height by an electromagnet. Turning off the electromagnet releases the ball, which passes through the light gates positioned at d1 and d2 respectively. When the ball passes a light gate, it records the time at which it passes.
My values of instantaneous accelerations are coming out just fine. The part where I am facing trouble is when trying to determine it from the slopes of the graphs of velocity vs time, or position vs time squares, or the square of velocity vs position.
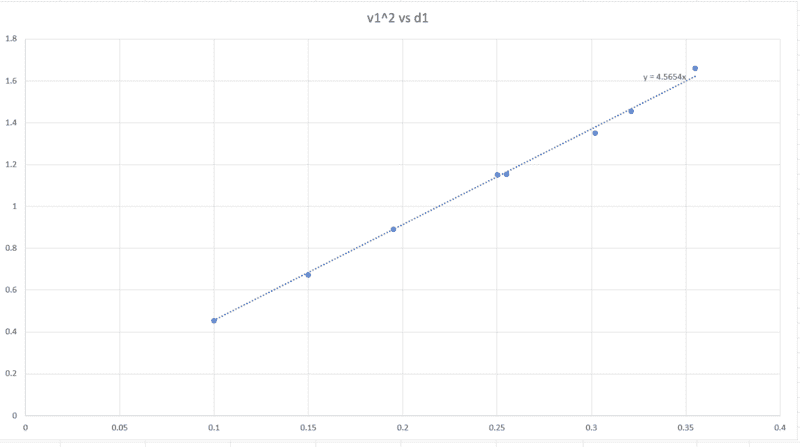
for instance, the slope of the graph of v1^2 vs d1 (attached) is coming out to be 4.5654. Comparing this with the kinematic equation v^2 = 2gh, 2g = 4.5654, which means g = 4.5654/2, which is not even remotely close to the accepted value of g. Where am I going wrong?

 

[nasu]

How do you get the values for the velocity v₁?

 

[gmax137]

Can you show d1 and d2 on your sketch? are they measured "down" from the initial ball position? Are the units in centimeters correct (those seem like very small distances).

 

[kuruman]

I will rephrase @nasu's question.

Why do you need to get the values for v₁? Can you find an expression for $g$ in terms of quantities that you measured directly? These are times and distances. What expression do you know that relates these two when an object is dropped from rest?

 

[acertainayush]

How do you get the values for the velocity v₁?

using d1/t1

Can you show d1 and d2 on your sketch? are they measured "down" from the initial ball position? Are the units in centimeters correct (those seem like very small distances).

i apologize for my mistake, values of d1 and d2 are in meter units

 

[kuruman]

using d1/t1

That's the average velocity, not the instantaneous velocity which is what appears in $v=\sqrt{2gd}.$ I suggest that you follow my recommendation in post #4.

 

[nasu]

Then what yo call v1 is the average velocity over the distance d1 and not the instantaneous velocity at the position of the first gate. If you use $v1^2=2ad_1$, $v_1$ should be the velocity after travelling the distance d1 and not the average.

 

[acertainayush]

I will rephrase @nasu's question.

Why do you need to get the values for v₁? Can you find an expression for $g$ in terms of quantities that you measured directly? These are times and distances. What expression do you know that relates these two when an object is dropped from rest?

thanks. so possible to find g from the slope of position vs time squared graph?

 

[nasu]

Why did you pick these pair of positions for the gates? Was there any plan here or you just picked some random values? If you want to use a graph of distance versus time, why not just one gate at various heights? What was the purpose of using two gates?

 

[acertainayush]

the relative positions of the gates were chosen randomly

 

[kuruman]

thanks. so possible to find g from the slope of position vs time squared graph?

Yes.

 

[gmax137]

What was the purpose of using two gates?

I think this is an important question, and the OP needs to understand the answer.

 

[BvU]

thanks. so possible to find g from the slope of position vs time squared graph?

Why ask ? Try it !

the relative positions of the gates were chosen randomly

I sense a typical case of following lab instructions without any preliminary thinking -- correct me if I am wrong ( I hope I am !)

To be of useful assistance we would need to know a little more about your context: at what point you are in class. Because the quote 'find g from the slope of position vs time squared graph' makes me guess that you know about what we call the SUVAT equations, in particular $s = {1\over 2} at^2 .\quad$ Do you ?

 

[jbriggs444]

As I read the data table and the drawing, you are adopting a downward = positive coordinate system with the origin at the electromagnet.

$d_1$ is the position of the top gate (in cm)
$d_2$ is the position of the bottom gate (in cm)
$h$ is the difference: $d_2 - d_1$ (converted to meters)
$t_1$ is the time at the first gate (in seconds as per the column heading)
$t_2$ is the time at the second gate (in seconds as per the column heading).
$t$ is $t_2 - t_1$

We are not told whether the time coordinates are accurate relative to a drop time at $t_0 = 0$ or are if the drop time is only approximately zero.

We can attempt some rudimentary analysis to confirm the interpretation of the columns.

First line: 0.2373 seconds for a drop of 0.255 cm. In 0.2373 seconds at 9.8 meters/second squared we should have managed $\frac{1}{2}at^2$ = 27 centimeters of drop.

No. That is unrealistic. But suppose that $d_1$ is actually expressed in meters. 27 centimeters is close to 25.5 centimeters. So let us proceed on this assumption.

First line: 0.4254 seconds for a drop of 0.84 meters. $\frac{1}{2}at^2$ = 0.89 meters. That is a reasonable match as well.

Which means that the "height" column is also off by a factor of 100.

It looks like our time readings quoted to four places are good to something a bit less than 2 significant digits. The zero point on the readings may be off. This may be a random error. Or it may be a systematic error.

Second line: We have 0.1828 seconds for a drop of 15 centimeters. $\frac{1}{2}at^2$ = 16.3 cm.

Predicted distances seem to be about 6 to 8% high. So the measured times must be 3 or 4% low. We could look at the remaining lines to see how consistent the error is. But let us cut to the chase.

Conclusion: We cannot assume that the time of the drop is zero.

No matter. We are after a formula that can take the elapsed time between the ball passing two measured displacements and calculate an acceleration from that.

Strategy:

1. Write down a formula for the expected elapsed time between passing the two measured displacements from the drop point in terms of those displacements and the unknown acceleration of gravity.$$t_\text{elapsed} = \text{something involving } a, d_1 \text{ and } d_2$$
2. Solve that equation for the acceleration of gravity in terms of the measured elapsed time and the two measured displacements.

Your task is to figure out a formula for step 1 above.