kvdr
- 4
- 1
- TL;DR Summary
- Question about stronger relativity paradox than twin paradox.
The twin paradox can be explained by changing reference frames. But I’m really curious how this paradox can be explained.
In the situation below there are three observers:
So, what does every observer see:
Can someone please explain what really happens and how that is in accordance with relativity theory.
Thank you!
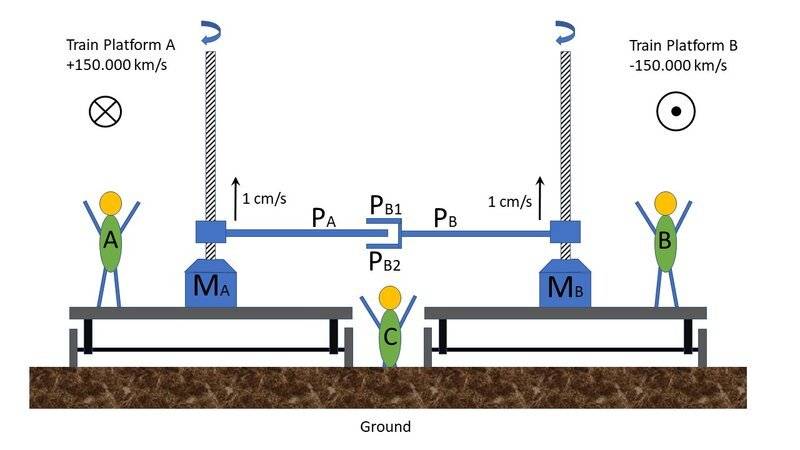
In the situation below there are three observers:
- A: Standing at a moving train platform moving at a speed of c/2 relative to “the ground”.
- B: Standing at a moving train platform moving at a speed of c/2 relative to “the ground”, but in the opposite direction as A.
- C: Does not move against the ground.
So, what does every observer see:
- C: A and B move at the same speed (in opposite directions) relative to C, so plate PA stays between PB1 and PB2. => nothing breaks
- A: sees that B moves at high speed. According the relativity theory everything on platform B is going slower. So, the upward speed of plate PB (1 cm/s) will also be lower. Therefore, plate PA will bump against plate PB1. => plate PB1 breaks
- B: sees that A moves at high speed. According the relativity theory everything on platform A is going slower. So, the upward speed of plate PA (1 cm/s) will also be lower. Therefore, plate PB2 will bump against plate PA. => plate PB2 breaks
Can someone please explain what really happens and how that is in accordance with relativity theory.
Thank you!