Explaining Dimensions of Tanagrams Without Midpoint Assumptions

[jljarrett18]

I am currently working on an assignment using Tanagrams. I have the information that I have:
• 2 large, and congruent, isosceles right triangles
• 1 medium isosceles right triangle
• 2 small, and congruent, isosceles right triangles
• 1 square
• 1 parallelogram

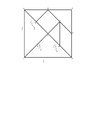
The pieces can be rearranged with no gaps or overlapping of shapes into a square with dimensions 1 unit by 1 unit (i.e., the entire area of the square is 1 unit^{2})

I have figured out all the dimensions of the pieces but I need to explain how I came up with them. The only thing is you cannot make midpoint assumptions (e.g. B is the midpoint between A and C). I used this assumption in determining the dimensions so I need a new way to explain the dimensions. I have already explained how I got the 2 large congruent isosceles triangles, but I am stuck.
I have attached a picture of the tanagram

This is what I have so far for my explanation:

The way that I determined the dimensions of each of the 7 shapes was by the information within the task. The information given says that the dimension of the whole square is 1 unit by 1 unit. So for the two large congruent isosceles triangles (segment AJ and JK) the one side is 1 unit because the one side takes up the whole side of the square as you can see by the 1 in red. Next, I tried to determine the dimension of the other two legs. By Theorem 6 of Pythagorean theorem: A triangle is a right triangle if and only if the sum of the squares of the two smaller legs equal the square of the largest leg; so (UCertify, n.a). Next what I did was plugged in 1 for C and squared it which is 1. Since the triangles are isosceles that mean both sides are congruent and equal. So, I divided 1 by 2 and then took the square root to find out what the two sides are which are

 

[Opalg]

What you have done so far is to identify the dimensions of the two big triangles $AFJ$ and $JFK$. I think that you should next look at the square $BDFE$. Draw its diagonal $BF$. You know that $F$ is the centre of the square $ACKJ$, and you know that the angles $BFD$ and $FAJ$ are both $45^\circ$. It follows that $BF$ is parallel to $AJ$, and you should be able to conclude that the length of $BF$ is $\frac12$. Then use Pythagoras to find the lengths of the sides of the square $BDFE$, and deduce that $B$ is indeed the midpoint of $AC.$

[Spelling suggestion: the name of these shapes is Tangrams, with two a's, not three.]

 

[jljarrett18]

So now I can prove the dimensions of square are (√2)/4. With that information I then can fill in the rest of the shapes of the tangrams because I know one length of the square?