- #1
jljarrett18
- 15
- 0
I am currently working on a task involving isometries. I am confused as to how to explain the next two tasks to my adviser.
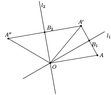
B. Any combination of isometries can be accomplished with one of the four fundamental isometries (i.e., translation, reflection, rotation, or glide reflection). Provide a logical argument that demonstrates that, given any pair of reflections, there exists a rotation or translation that produces the same result.
C. Demonstrate, using a counter example, that the product of a pair of isometries A and B is not always commutative (i.e., AB does not always equal BA).
B. Any combination of isometries can be accomplished with one of the four fundamental isometries (i.e., translation, reflection, rotation, or glide reflection). Provide a logical argument that demonstrates that, given any pair of reflections, there exists a rotation or translation that produces the same result.
C. Demonstrate, using a counter example, that the product of a pair of isometries A and B is not always commutative (i.e., AB does not always equal BA).