Explaining Proof of Quick-Sort's O(nlog n) Expected Running Time

[evinda]

Hello! (Wave)

View attachment 4422

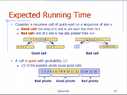
View attachment 4423I am trying to understand the proof that the expected running time of quick-sort is $O(n \log n)$.

Could you maybe explain it to me?

 

[evinda]

Suppose that we use the following algorithm:

Quicksort(S):
1.  if S contains at most one element then return S
    else
2.       choose an element a randomly from S;
3.       let S1, S2, and S3 be the sequences of elements in S less than, equal to, and greater than a, respectively;
4.       return Quicksort(S1) followed by S2 followed by Quicksort(S3)

I have tried the following:

Let $$T(n)$$ be the expected time required by the Quicksort algorithm in order to sort a sequence of $$n$$ elements. We have that $$T(0)=T(1)=b$$ for a constant $$b$$.

We suppose that the elements $$a$$ is the $$i$$-th smallest elements of the $$n$$ elements of the sequence $$S$$.
Then the 2 recursive calls of Quicksort have expected time $$T(i-1)$$ and $$T(n-i)$$, respectively.
Since the lines 2-3 require time $$O(n)$$ and the line 1 requires time $$O(1)$$, we have the following recurrence relation:

$$T(n) \leq cn+ \frac{1}{n} \sum_{i=1}^n \left[ T(i-1)+T(n-i)\right], n \geq 2$$

$$\\ T(n) \leq cn+ \frac{1}{n} \sum_{i=1}^n \left[ T(i-1)+T(n-i)\right] \\ \leq cn+ \frac{1}{n} \sum_{i=1}^n \left[ 2T(i-1) \right] =cn+ \frac{2}{n} \sum_{i=0}^{n-1} T(i) \\ \Rightarrow T(n) \leq cn+ \frac{2}{n} \sum_{i=0}^{n-1} T(i)(1)$$

We will show that for $$n \geq 2$$, $$T(n) \leq k n \log n$$, for $$k=2(c+b)$$ positive.

For $$n=2$$: From the relation (1) we have $$T(2) \leq c2+ 2b=2(c+b) \checkmark$$

We suppose that $$T(n) \leq k n \log n$$ γfor some $$n \geq 2$$.

We will show that $$T(n+1) \leq k (n+1) \log (n+1)$$ .

From the relation (1) we have $$T(n+1) \leq c(n+1)+ \frac{2}{n+1} \sum_{i=0}^{n} T(i) \leq c(n+1)+ \frac{2}{n+1} (n+1) T(n)= c(n+1)+2T(n) \leq c(n+1)+2 k n \log n \leq (n+1) (c+2k \log n)$$How could we continue? Or should we use strong induction?