- #36
Adit Thurumalla
- 2
- 0
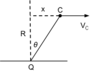
The COG CAN be considered as an axis of rotation. What else could one possibly consider as an axis of rotation? The mathematics would be least complicated when the axis of rotation passes through COG and perpendicular to the plane of the surface of the coin.ObjectivelyRational said:How would you respond to a student who raises the issue of "frame of reference" for which the definition of "axis of rotation" is made?
For example if a student said in the context of a coin rolling on a table at a constant velocity, "What about from the frame of reference of the center of gravity of the coin? The table is moving in a straight line relative to the COG, the edge is moving without slipping at the same speed as the table, but the coin is rotating about the COG which is stationary (translationally). Why in this frame of reference should the COG not be considered the axis of rotation?"
How would/should you respond?