Explaining the Cross Product for Two Vectors

[member 731016]

Homework Statement

Trying to find whether there is a vector that can solve the cross product between two vectors.

Relevant Equations

Cross product formula: A cross B = ABcos(theta)
Dot product formula: A dot B = ABsin(theta)

Hi!

For this problem,

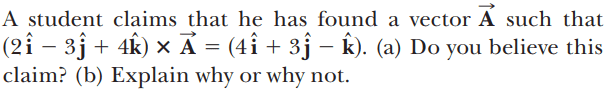
The solution is,

However, I don't understand their solution at all. Can somebody please explain their reasoning in more detail.

Many thanks!

 

[TSny]

If $\mathbf{B} \times \mathbf{A} = \mathbf{C}$, what is the angle between $\mathbf{B}$ and $\mathbf{C}$ (assuming $\mathbf{C} \neq 0$)?

 

[member 731016]

Thank for your reply! 90 degrees I think because the cross product of two vector is always perpendicular to the plane formed by the two vectors. Many thanks!

 

[member 731016]

Thanks, I see now, so since B and C must be at 90 degrees for it to be a cross product then we take the scalar product to find whether there is any component of B on C or C on B. And the scalar product of all components must be zero if B and C are to be perpendicular. Do you please know what we call it when the B and C are not 90 degrees to each other?Many thanks!

 

[haruspex]

Cross product formula: A cross B = ABcos(theta)
Dot product formula: A dot B = ABsin(theta)

Assuming θ is the angle between the vectors, you have that, ahem, crossed.
$||\vec A\times\vec B||=||\vec A||.||\vec B||.| \sin(\theta)|$
$||\vec A.\vec B||=||\vec A||.||\vec B||.| \cos(\theta)|$.

the scalar product of all components must be zero

That wording suggests a misunderstanding. The scalar product of two vectors is a single number. There is not a separate scalar product for each component.

what we call it when the B and C are not 90 degrees to each other?

Do you mean for two vectors in general? Maybe "non orthogonal"? Not aware of anything more concise.

 

[member 731016]

Assuming θ is the angle between the vectors, you have that, ahem, crossed.
$||\vec A\times\vec B||=||\vec A||.||\vec B||.| \sin(\theta)|$
$||\vec A.\vec B||=||\vec A||.||\vec B||.| \cos(\theta)|$.That wording suggests a misunderstanding. The scalar product of two vectors is a single number. There is not a separate scalar product for each component.Do you mean for two vectors in general? Maybe "non orthogonal"? Not aware of anything more concise.

Thanks for your reply! Sorry, what did you please mean when you said that we cannot take the scalar product of each component. My textbooks shows:

Many thanks!

 

[member 731016]

Do you mean for two vectors in general? Maybe "non orthogonal"? Not aware of anything more concise.

Yeah, thanks I mean for any two vectors in general. I think cross product is orthogonal. Many thanks!

 

[haruspex]

what did you please mean when you said that we cannot take the scalar product of each component

Sorry, I didn’t manage to express that quite correctly.
Your remark in post #4 implies you think that if $\vec x=x_i\vec i+x_j\vec j+x_k\vec k$ and $\vec y=y_i\vec i+y_j\vec j+y_k\vec k$ are orthogonal then each of the scalar products $x_i\vec i.y_i\vec i$, $x_j\vec j.y_j\vec j$, etc., must be zero. My point is that the scalar product $\vec x.\vec y$ is the sum of those individual products, and it is only that sum that needs to be zero.

 

[member 731016]

All goods, thanks for your reply!

If vectors x and y are not orthogonal, then we can't call it a cross product since the vectors are not at right angles. Is there a specific term used for non-orthogonal vectors?

Many thanks!

 

[haruspex]

Is there a specific term used for non-orthogonal vectors?

Not that I am aware of.

 

[member 731016]

Not that I am aware of.

Ok thank you!

 

[Orodruin]

Assuming θ is the angle between the vectors, you have that, ahem, crossed.
$||\vec A\times\vec B||=||\vec A||.||\vec B||.| \sin(\theta)|$
$||\vec A.\vec B||=||\vec A||.||\vec B||.| \cos(\theta)|$.

Pet peeve: The appropriate LaTeX for the dot product is \cdot. Norms are preferably typeset with \| or \lVert and \rVert.
$$
\vec A \cdot \vec B = \|\vec A\| \|\vec B\| \cos\theta
$$