- #1
sponsoredwalk
- 533
- 5
I have posted this here for two reasons, one I think you all will really appreciate this
as a teaching tool to hopefully increase your students understanding (and hopefully
grades) & second because you all might find/make more concept maps on more
advanced topics or with focus shifted in a different direction (i.e. a concept map
of theorems for example!). Please if you ever come across or make anything of the sort
please share it here & we'll hopefully amass quite a collection. References to books
containing concept maps more than welcome too!
I have become convinced of the power of concept maps as a way to
truly understand a subject. Please allow me to convince you with this
opening post then as payment for this miraculous gift I am giving you
I merely request you make/give/find me concept maps on areas of
mathematics such as:
Here's an elementary image of a concept map in real analysis:
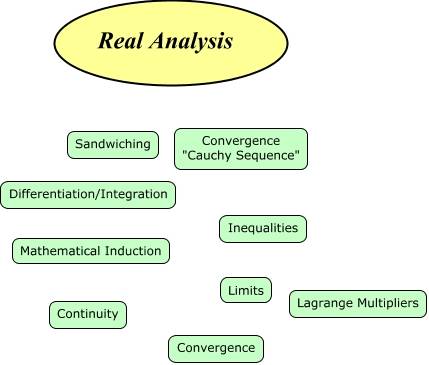
Not very convincing is it? Not very powerful or illuminating, I mean you
can look in the cover of your book & see this & it's probably the image of
a concept map a lot of us would think of, something not very informative.
However, look how powerful a concept map can become!
That is the kind of knowledge it would take over 100 pages, and some
serious thought, to acquire & to be honest diff eq's aren't fun because
this is precisely the knowledge you gain after all that hard work! The
fun should be devoted to the theorems holding differential equations
together (You know when you read a book & some author will put in brackets the word
"proof?" after a statement sometimes, I do it with "concept map?"). So to repeat, the
fun should be devoted to the theorems holding differential equations
together (concept map?).
If that one didn't convince you it's probably because there was some
detail missing in it, here's a more complete version:
Now, there may be a few bits and bobs missing, still if you were able to
approach the subject knowing that this is the general form you're striving
for with 1st order ode's that are solvable without recourse to numerical
methods you'd be pretty confident!
I took those pictures from this pdf file, there are more concept maps in it
on differential equations. Looks just fantastic!
Still, these concept maps illustrate the complexity of the subjects you're
trying to master, it's bad enough meeting all these new concepts in one
go but you also have to make sense of how they all fit together & how
they interconnect. Here is a drastic illustration of the complex web of
interconnectedness a subject (Linear Algebra) can contain:(Download that picture or use firefox zoom or something to examine
that beast! taken from here). Still, I've actually learned from just looking at that
picture! Made sense instantly!
Still, a theorem-interconnectedness concept map would be even more
useful & revealing! For example in my naivety I didn't fully understand
how a subspace of a vector space can be validated just by using λa + b,
I mean there's a nice way to build up to that by proving, I think, two or
three previous theorems.
Now, I want to emphasize the main reason why I think this is so important is because
it illuminates why a book is structured the way it is. In electromagnetism, a subject I
have yet to study properly, I have been slowly finding out about it but a lot of it is in
the dark & I don't have the time to do it properly. Still looking at the following concept
map
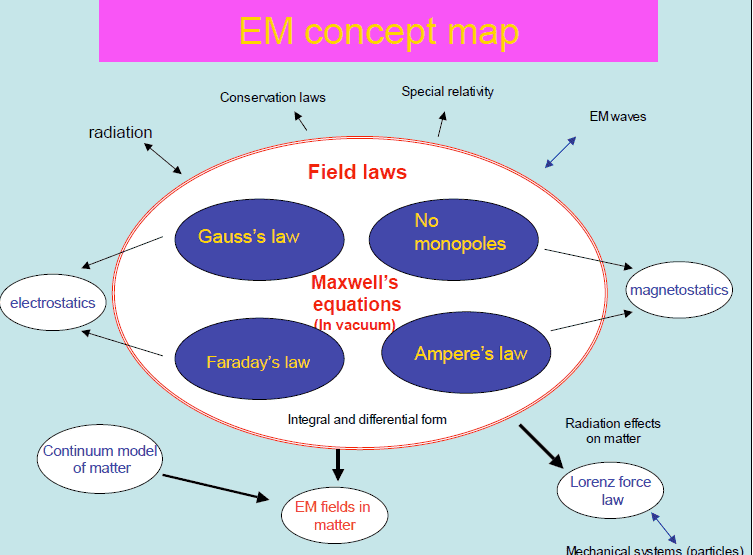
and more of it makes sense now (that Gauss & Faraday are for electrostatics &
Amere is for magnetostatics, taken from here). This is tiny but that's because the concept map here
contains nothing compared to the differential equations map above! I'd make more
connections if the map was better! It would just clarify why the book is structured the
way it is, I know nothing substantial about E&M, nothing, but if I can get some grasp
on where I'm going as regards concepts it would help. This is universally true, in
advanced mathematics especially! Something like this:
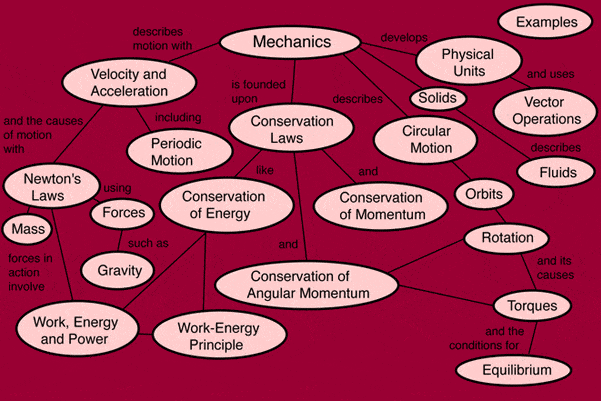
contains info on where you're going in elementary mechanics, but I mean concept maps
on moment of inertia in various situations, or friction situations etc... could be made
too! That's the stuff people have trouble with & for which a map would help make
sense out of!
Hopefully I've made my case, I'd be interested in opinions on this, here are a few of
the links I've found that contain useful info & maps that some people might appreciate:
http://www.merga.net.au/documents/RP562006.pdf
http://cmc.ihmc.us/papers/cmc2004-271.pdf
link
http://www.informaworld.com/smpp/section?content=a916574853&fulltext=713240928#references
http://www.mtedu.tmue.edu.tw/leeys_teaching/%E7%A0%94%E8%A8%8E%E6%9C%83/PME/PME32%282008%29/Volumen%204/Research_Reports,_vol._4-36.pdf
The idea of concept maps within concept maps within concept maps
within a locker in the film Men in Black isn't such a weird thought for a
person to have anymore, is it?
as a teaching tool to hopefully increase your students understanding (and hopefully
grades) & second because you all might find/make more concept maps on more
advanced topics or with focus shifted in a different direction (i.e. a concept map
of theorems for example!). Please if you ever come across or make anything of the sort
please share it here & we'll hopefully amass quite a collection. References to books
containing concept maps more than welcome too!
I have become convinced of the power of concept maps as a way to
truly understand a subject. Please allow me to convince you with this
opening post then as payment for this miraculous gift I am giving you
I merely request you make/give/find me concept maps on areas of
mathematics such as:
------------------metric spaces, elementary fixed point theory, partial differential equations, elementary differential geometry, modern diff geom, measure theory & Lebesgue integration, modern geometry, elementary probability & statistics, modern probability & statistics, lie theory, abstract algebra, topology,
differential topology, algebraic topology, algebraic geometry, whatever else!
Here's an elementary image of a concept map in real analysis:
Not very convincing is it? Not very powerful or illuminating, I mean you
can look in the cover of your book & see this & it's probably the image of
a concept map a lot of us would think of, something not very informative.
However, look how powerful a concept map can become!
That is the kind of knowledge it would take over 100 pages, and some
serious thought, to acquire & to be honest diff eq's aren't fun because
this is precisely the knowledge you gain after all that hard work! The
fun should be devoted to the theorems holding differential equations
together (You know when you read a book & some author will put in brackets the word
"proof?" after a statement sometimes, I do it with "concept map?"). So to repeat, the
fun should be devoted to the theorems holding differential equations
together (concept map?).
If that one didn't convince you it's probably because there was some
detail missing in it, here's a more complete version:
Now, there may be a few bits and bobs missing, still if you were able to
approach the subject knowing that this is the general form you're striving
for with 1st order ode's that are solvable without recourse to numerical
methods you'd be pretty confident!
I took those pictures from this pdf file, there are more concept maps in it
on differential equations. Looks just fantastic!
Still, these concept maps illustrate the complexity of the subjects you're
trying to master, it's bad enough meeting all these new concepts in one
go but you also have to make sense of how they all fit together & how
they interconnect. Here is a drastic illustration of the complex web of
interconnectedness a subject (Linear Algebra) can contain:(Download that picture or use firefox zoom or something to examine
that beast! taken from here). Still, I've actually learned from just looking at that
picture! Made sense instantly!
Still, a theorem-interconnectedness concept map would be even more
useful & revealing! For example in my naivety I didn't fully understand
how a subspace of a vector space can be validated just by using λa + b,
I mean there's a nice way to build up to that by proving, I think, two or
three previous theorems.
Now, I want to emphasize the main reason why I think this is so important is because
it illuminates why a book is structured the way it is. In electromagnetism, a subject I
have yet to study properly, I have been slowly finding out about it but a lot of it is in
the dark & I don't have the time to do it properly. Still looking at the following concept
map
and more of it makes sense now (that Gauss & Faraday are for electrostatics &
Amere is for magnetostatics, taken from here). This is tiny but that's because the concept map here
contains nothing compared to the differential equations map above! I'd make more
connections if the map was better! It would just clarify why the book is structured the
way it is, I know nothing substantial about E&M, nothing, but if I can get some grasp
on where I'm going as regards concepts it would help. This is universally true, in
advanced mathematics especially! Something like this:
contains info on where you're going in elementary mechanics, but I mean concept maps
on moment of inertia in various situations, or friction situations etc... could be made
too! That's the stuff people have trouble with & for which a map would help make
sense out of!
Hopefully I've made my case, I'd be interested in opinions on this, here are a few of
the links I've found that contain useful info & maps that some people might appreciate:
http://www.merga.net.au/documents/RP562006.pdf
http://cmc.ihmc.us/papers/cmc2004-271.pdf
link
http://www.informaworld.com/smpp/section?content=a916574853&fulltext=713240928#references
http://www.mtedu.tmue.edu.tw/leeys_teaching/%E7%A0%94%E8%A8%8E%E6%9C%83/PME/PME32%282008%29/Volumen%204/Research_Reports,_vol._4-36.pdf
The idea of concept maps within concept maps within concept maps
within a locker in the film Men in Black isn't such a weird thought for a
person to have anymore, is it?

Last edited by a moderator: