Exploring a QM particle in Motion with GR

[PRB147]

I encountered a problem in reading Phys.Lett.B Vol.755, 367-370 (2016).
I cannot derive Eq.(7), the following snapshot is the paper and my oen derivation,
I cannot repeat Eq.(7) in the paper.

$g^{\mu\nu}$ is diagonal metric tensor and$g^{\mu\mu}$ is the function of $\mu$ only, $\mu=x,y,z$.
My derivation is as follows, but I cannot repeat their result and my result contains the cross term differential $\partial_x \partial_y$.

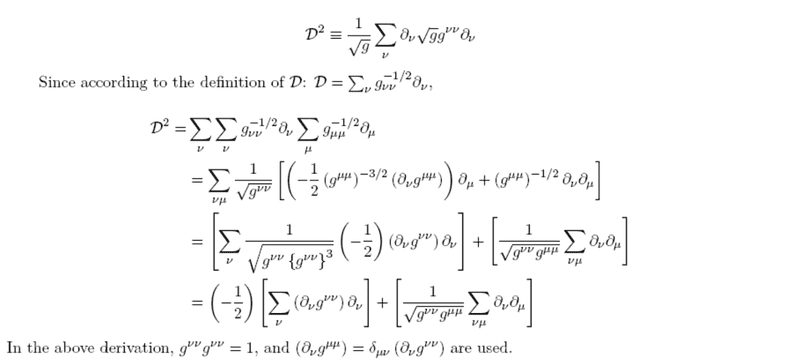
(The first line is their result), while the last line is mine.
Would anyone can help me to elucidate this problem?

 

[malawi_glenn]

What does the three horizontal lines after $\mathcal{D}^2$ mean in eq 7? It sometimes means that something is true by definition (identical to) https://en.wikipedia.org/wiki/Triple_bar

If this is the case, you can not derive eq. 7.

andgμμ is the function of μ only

indices are not variables, thus the metric is not a function of µ.

 

[Demystifier]

I cannot derive Eq.(7)

That's because the equation that precedes (7), namely ${\cal D}=\sum_{\nu}g_{\nu\nu}^{-1/2}\partial_{\nu}$, is a nonsense. And it seems that the authors of the paper are not well versed in tensor calculus. To see how Eq. (7) should be correctly written and derived, google Laplace-Beltrami operator.

 

[PeterDonis]

My derivation is as follows

Please use the PF LaTeX feature to post equations directly, not as images. There is a LaTeX Guide link at the lower left of each post window.

 

[PRB147]

What does the three horizontal lines after $\mathcal{D}^2$ mean in eq 7? It sometimes means that something is true by definition (identical to) https://en.wikipedia.org/wiki/Triple_bar

If this is the case, you can not derive eq. 7.indices are not variables, thus the metric is not a function of µ.

thank you for your comment, I thought the author's meaning is $g_{xx}$ depends only on x; $g_{yy}$ depends only on y; etc.

 

[PRB147]

That's because the equation that precedes (7), namely ${\cal D}=\sum_{\nu}g_{\nu\nu}^{-1/2}\partial_{\nu}$, is a nonsense. And it seems that the authors of the paper are not well versed in tensor calculus. To see how Eq. (7) should be correctly written and derived, google Laplace-Beltrami operator.

Thank you very much, I will read the relevant references according to your guidance.

 

[PeterDonis]

@PRB147, your posts #5 and #6 are a mess. Please pay more attention to proper quoting and formatting.

 

[PeterDonis]

@PRB147, your posts #5 and #6 are a mess.

Well, they aren't now because I have used magic moderator powers to edit them and clean them up. But my advice still stands.

 

[malawi_glenn]

thank you for your comment, I thought the author's meaning is $g_{xx}$ depends only on x; $g_{yy}$ depends only on y; etc.

No it does not...