Exploring Acceleration at Contact Point Between Wheel and Surface

[greg_rack]

Hello guys,

I am getting more and more confused each time I try to get a definitive answer on this doubt: what's the acceleration at the contact point between a surface and a wheel spinning on it(without slipping).
Considering this standard FBD for the above-described situation,

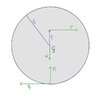(the direction of friction is just assumed to be as such)

are we able to know a-priori the acceleration at the contact point(let's say A)?
Intuitively I wouldn't say so, since instantaneously point A is moving at 0 velocity but about to change it; so how could the acceleration be also 0? My guess is, thus, that it should be calculated using the relative motion equations derived for rigid bodies.

But often, a necessary kinematic conditions for such problems is to assume $a_A=0$, and in some textbooks it is explicitly stated but, in my opinion, without further clarifications... almost as a given, but which for me, sounds all but a given :)

I'd be glad if you help me clarify this once and for all; also, what happens exactly to the velocity at A? Is it really 0 at that moment?

 

[BvU]

Hi,

I can see you are confused . You have a drawing where things are left to guessing. What is $T$ ? $r_1$ ? $\omega$ (or is it $w$) ? $G$ ?
It's reasonable to assume the surface is at the bottom , so let's do that.

What way is the acceleration, if you have to guess ? So what way does $F_f$ probably point ?
(check: what happens if slipping is about to occur because of excessive acceleration ? -- or conversely: what way is the acceleration if there is NO friction at all ?)

Note that your point A can not be marked with a pen: it moves on the surface and it moves on the wheel. If you mark a point on the rim of the wheel it will describe a cycloid.

$\$

 

[greg_rack]

Hi,

I can see you are confused . You have a drawing where things are left to guessing. What is $T$ ? $r_1$ ? $\omega$ (or is it $w$) ? $G$ ?
It's reasonable to assume the surface is at the bottom , so let's do that.

What way is the acceleration, if you have to guess ? So what way does $F_f$ probably point ?
(check: what happens if slipping is about to occur because of excessive acceleration ? -- or conversely: what way is the acceleration if there is NO friction at all ?)

Note that your point A can not be marked with a pen: it moves on the surface and it moves on the wheel. If you mark a point on the rim of the wheel it will describe a cycloid.

Actually you are very right:
that $\omega$ is of course $w$, the weight. $T$ is an applied external force, at distance $r_1$ from the centre, whilst G is the centroid of the wheel and thus its center of gravity... and the surface is, indeed, at the bottom

If I were to guess the direction of the acceleration, the following would be my reasoning:
force $T$ would be causing a clockwise rotation, thus with respect to the surface, point A would be instantaneously moving(with velocity pointing) to the left, causing the friction force acting on the wheel to the right.

If there were instead to be no friction, the acceleration at the contact point would be 0 as well; but that sounds quite counter-intuitive to me for friction to be 0.
If slipping was about to occur, $F=\mu_s N$ being N the normal force.

 

[BvU]

Actually you are very right:
that $\omega$ is of course $w$, the weight. $T$ is an applied external force, at distance $r_1$ from the centre, whilst G is the centroid of the wheel and thus its center of gravity... and the surface is, indeed, at the bottom

Don't worry, I guessed as much

If I were to guess the direction of the acceleration, the following would be my reasoning:
force $T$ would be causing a clockwise rotation, thus with respect to the surface, point A would be instantaneously moving(with velocity pointing) to the left, causing the friction force acting on the wheel to the right.

Ah! but weren't we focusing on a non-slip situation ? In which case neither the point A nor the mark on the rim of the wheel at point A can move to the left !

If there were instead to be no friction, the acceleration at the contact point would be 0 as well; but that sounds quite counter-intuitive to me for friction to be 0.

Correct. Wheel on ice is the example. Point A does not move, mark on rim moves to the left.

If slipping was about to occur, $F=\mu_s N$ being N the normal force.

Correct as well ! And at that point the acceleration is still to the right, and its magnitude is $/A = F/m$.

$\$

 

[greg_rack]

In which case neither the point A nor the mark on the rim of the wheel at point A can move to the left !

Sorry, I think I am missing up on your distinction between "point A" and "mark on the rim at point A".
Aren't we always referring to the "mark on the rim at point A", in other words, the IC for a given instant?

And also, what do you mean by "In a non-slip case, neither point A nor the mark can move to the left"?
I'm starting to think I'm lacking of some background "visualization" of the concept... moreover why, if on ice, would the mark move to the left?

 

[Lnewqban]

The acceleration of point A respect to the road should have its maximum value when it is in contact with it, and its velocity should be zero.
The acceleration of point A should have its minimum value when it reaches the highest point of the cycloid respect to the road, and the value of its velocity should be maximum at there.

 

[BvU]

It seems we have painted ourselves in a corner by not clearly defining point A. In #2 I interpreted it as the point of contact, but it may be better to actually mark a dot on the rim of the wheel and mark that with a painted A. That way we keep @Lnewqban on board .

Sorry, I think I am missing up on your distinction between "point A" and "mark on the rim at point A".
Aren't we always referring to the "mark on the rim at point A", in other words, the IC for a given instant?

And also, what do you mean by "In a non-slip case, neither point A nor the mark can move to the left"?
I'm starting to think I'm lacking of some background "visualization" of the concept... moreover why, if on ice, would the mark move to the left?

Hehe, my turn to be confused: what does IC stand for (Integrated circuit, Intensive care, inner circle, in casu, ...) ?

For the case when there is no slipping, the mark on the rim (which was at the contact point in the drawing) moves upward. It does not move to the left. The point of contact also moves to the right.

When there is no friction I have to correct myself: I overlooked/misinterpreted your definition of $T$

$T$ is an applied external force, at distance $r_1$ from the centre,

I mistakenly interpreted $\ { \bf r } \times \vec T\$ as a torque around $G$ (as if we were pedaling on a bicycle). But your definition is clear -- isn't it ? The way you draw it, it is as if someone, fixed wrt the floor, is pulling a rope to the right. The rope is wound around a disc with radius $r_1$. Let's check a few cases:

• $r_1 = 0$, no friction. What happens? The whole wheel accelerates to the right without rotating.
• $0 < r_1$, no friction. The whole wheel accelerates to the right and starts rotating clockwise around G (in the reference frame of the wheel, which is a non-inertial reference frame).

There will be an intermediate value of $r_1$ for which the acceleration of the wheel and the angular acceleration times $r_2$ are equal: rolling without slipping on a frictionless surface ! In billiards it's called the sweet spot, but for a sphere $I=\frac 2 5 \, mr^2$. For a cylinder it is $I=\frac 1 2 \, mr^2$, so if $r_1 = \frac 1 2 \,r_2$ .

This way we have specified

• $0 < r_1 < \frac {r_2} 2$, no friction. The whole wheel accelerates to the right and starts rotating clockwise around G (in the reference frame of the wheel, which is a non-inertial reference frame). The rotations do not keep up with the movement of the center of mass and a point on the rim will slip to the right when at the bottom
• $\frac {r_2} 2 < r_1 < r_2$, no friction. The whole wheel accelerates to the right and starts rotating clockwise around G (in the reference frame of the wheel, which is a non-inertial reference frame). The rotations accelerate faster than the center of mass and a point on the rim will slip to the left when at the bottom

---

Interesting would also be to study the case that the line of action of $t$ is below $G$ ! (kind of a $r_1 < 0$ )

---

And now the "with friction" situation ...
$\Bigl($ left for later: I'm exhausting meself and there will be questions (I hope ) and corrections (I fear ) $\Bigr)$

$\$

 

[A.T.]

The acceleration of point A respect to the road ...

What do you mean by "acceleration respect to the road"? Acceleration is frame invariant across inertial frames, so it's the same in the rest frame of the road as it is in the rest frame of the wheel center (assuming rolling at constant speed)

... should have its maximum value when it is in contact with it, and its velocity should be zero.
The acceleration of point A should have its minimum value when it reaches the highest point of the cycloid respect to the road, and the value of its velocity should be maximum at there.

No, see above. Since the acceleration has a constant magnitude in the rest frame of the wheel center, it has the same constant magnitude in the rest frame of the road. You seem to confuse path curvature with acceleration, while ignoring the varying speed along the path.

 

[wrobel]

https://www.physicsforums.com/insights/rare-kinematic-formula/

 

[greg_rack]

Guys I am sorry, but I feel like I'm even more confused now...
The original question was just:
why is the horizontal component of the acceleration at the contact point(call it A) $a_{Ax}=0$, in a wheel spinning -without slipping- on a surface?
It seems we have been losing quite some contact with it.

 

[greg_rack]

And now the "with friction" situation ...
$\Bigl($ left for later: I'm exhausting meself and there will be questions (I hope ) and corrections (I fear ) $\Bigr)$

But, how can a wheel spin on a surface it there's no friction between the two?! Doesn't spinning and consequently translation occur because of friction? Because of "gripping" between the surface?
I see it this way but that might another wrong preconception; but aren't we able to walk just because of friction? So, how could a wheel move on ice?

 

[jbriggs444]

why is the horizontal component of the acceleration at the contact point(call it A) $a_{Ax}=0$, in a wheel spinning -without slipping- on a surface?

Because the vertical component is equal to the [constant] magnitude of the acceleration? So there is nothing left for the horizontal?

 

[A.T.]

why is the horizontal component of the acceleration at the contact point(call it A) $a_{Ax}=0$, in a wheel spinning -without slipping- on a surface?

Because the acceleration is always towards the center of the wheel:
https://en.wikipedia.org/wiki/Centripetal_force

 

[greg_rack]

Because the acceleration is always towards the center of the wheel:
https://en.wikipedia.org/wiki/Centripetal_force

But, say, a force keeps getting applied at distance $r_1$ from the center(even the weight in an inclined surface), wouldn't the tangential velocity increase and thus, wouldn't there also be a tangential acceleration?
I understand all particles on the wheel would only have a centripetal accel., but just for the non-accelerated case

 

[A.T.]

But, say, a force keeps getting applied at distance $r_1$ from the center(even the weight in an inclined surface), wouldn't the tangential velocity increase and thus, wouldn't there also be a tangential acceleration?

For that accelerated case you still have the same cycloid path, which is vertical at the lowest point. Since velocity is zero there, the acceleration perpendicular to the path (here horizontal) is also zero.
https://en.wikipedia.org/wiki/Acceleration#Tangential_and_centripetal_acceleration

 

[greg_rack]

For that accelerated case you still have the same cycloid path, which is vertical at the lowest point. Since velocity is zero there, the acceleration perpendicular to the path (here horizontal) is also zero.
https://en.wikipedia.org/wiki/Acceleration#Tangential_and_centripetal_acceleration

Oh, now I see, thank you!
And I also found this video which clarifies it even further

 

[A.T.]

Oh, now I see, thank you!
And I also found this video which clarifies it even further

Yes, nicely shows the constant acceleration magnitude for constant rolling speed. It would be even
better if it showed the wheel as well, so you could see that acceleration always points towards the wheel center.

 

[haruspex]

Yes, nicely shows the constant acceleration magnitude for constant rolling speed.

Just to add that the result still stands even if the wheel is accelerating.