- #1
CookieSalesman
- 103
- 5
In Quantum Mech. we learned about classical uncertainty, and then Heisenberg's uncertainty principle which comes from it.
The way it is in the book is, the preceding chapter talks about how the superposition of lots of waves ∑ gives you these groups, and things like group velocity comes from this. Basically "wave packets".
But what did NOT make any sense is in the next chapter the book talks about uncertainty relations.
So from an arbitrary superposition of many waves... The book has two images
1. The sum of all of them, so it looks like
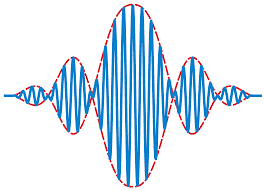
And then there's another one which plots Y (amplitude)) by K (wave number), which looks kind of like a very tall bell curve.
Okay I get it, picture 1 is just a sum/superposition of a bunch of different waves. I don't get what picture 2 is about (not shown). It simply plots amplitude by wave number. There are a few dots, the peak is marked with K=24π, Y=1. The two nearest points to the left and right are at 26pi and 22pi at Y=1/2.
Okay. I personally do not get why the the book is plotting Y by K but alright that's great. To me this is the most random graph you could possibly do. There's nothing else said about this.
Apparently I don't understand this well.
In the next chapter because the group of the superpositioned waves (picture 1) has a width of about ~1/12, and then the graph of amplitude by K is around 12. So voila
ΔKΔX~1
ΔwΔt~1 as well.
This makes NO sense to me, what just happened?
The book itself even explicates that we have written these as order of magnitude equations because the exact value of the products ΔkΔx and ΔwΔt depends on how the ranges are defined as well the shape of the packets. So what were the damn equations for...? Stupid book, take them back.
To me nothing is making sense anymore, particularly because the "width" of the amplitude (in picture 2, the bell-curve like picture) is just defined as the area where amplitude is greater than Y=1/2. If that's vague, it's kind of like when you look at a bell curve, and there's a portion of the graph demarcated by ±σ, containing some % of the entire curve. Who said you could just decide that the "width" of the curve which is graphed was defined this way?? What's the point of doing that as well?
I tried looking on Khanacademy and some MIT opencourse lectures but I do not think I found an explanation. I COULD watch a whole lecture, but I'm not entirely sure they answer my question. Nothing is explicitly under "classical uncertainty", as the book titles it. And the Heisenberg uncertainty is its own chapter.
Soon, k=2π/λ is derived, which gives dk=... and then ΔxΔλ~λ2/2π
Okay.. at least with this one I know where it's from.
Ultimately I think what explains why I'm confused is when the book gives an example...
Standing in a 20m long pier, you notice there are always 15 wave crests between the two ends of the pier.
Estimate the minimum uncertainty in the wavelength that could be computed.
Apparently it's 1cm.Huh...?
How does that even work?
I actually don't really get this. Just take a ruler and find the wavelength, what's the pier got to do with it? I understand that the more distance you have the better your accuracy but the big issue is that I don't even accept the existence of the equation which is used, ΔxΔλ because the book just pulled pulled some black magic and tossed this at me.
Ultimately I don't see how there is any "uncertainty" at all. I mean... just look at figure 1, where's the uncertainty? It looks pretty defined to me. I understand that I'm wrong, since this is just all fact but I'm struggling to justify the book's explanations. I'm doing my best to NOT just memorize equations and toss them out on exams.
So I'm just hoping that by giving lots of examples of why I'm confused it's helpful to you guys for understanding what the hell is confusing me, since I don't even know.
Please explain this to me or suggest some sources which could help.
Thanks.
The way it is in the book is, the preceding chapter talks about how the superposition of lots of waves ∑ gives you these groups, and things like group velocity comes from this. Basically "wave packets".
But what did NOT make any sense is in the next chapter the book talks about uncertainty relations.
So from an arbitrary superposition of many waves... The book has two images
1. The sum of all of them, so it looks like
And then there's another one which plots Y (amplitude)) by K (wave number), which looks kind of like a very tall bell curve.
Okay I get it, picture 1 is just a sum/superposition of a bunch of different waves. I don't get what picture 2 is about (not shown). It simply plots amplitude by wave number. There are a few dots, the peak is marked with K=24π, Y=1. The two nearest points to the left and right are at 26pi and 22pi at Y=1/2.
Okay. I personally do not get why the the book is plotting Y by K but alright that's great. To me this is the most random graph you could possibly do. There's nothing else said about this.
Apparently I don't understand this well.
In the next chapter because the group of the superpositioned waves (picture 1) has a width of about ~1/12, and then the graph of amplitude by K is around 12. So voila
ΔKΔX~1
ΔwΔt~1 as well.
This makes NO sense to me, what just happened?
The book itself even explicates that we have written these as order of magnitude equations because the exact value of the products ΔkΔx and ΔwΔt depends on how the ranges are defined as well the shape of the packets. So what were the damn equations for...? Stupid book, take them back.
To me nothing is making sense anymore, particularly because the "width" of the amplitude (in picture 2, the bell-curve like picture) is just defined as the area where amplitude is greater than Y=1/2. If that's vague, it's kind of like when you look at a bell curve, and there's a portion of the graph demarcated by ±σ, containing some % of the entire curve. Who said you could just decide that the "width" of the curve which is graphed was defined this way?? What's the point of doing that as well?
I tried looking on Khanacademy and some MIT opencourse lectures but I do not think I found an explanation. I COULD watch a whole lecture, but I'm not entirely sure they answer my question. Nothing is explicitly under "classical uncertainty", as the book titles it. And the Heisenberg uncertainty is its own chapter.
Soon, k=2π/λ is derived, which gives dk=... and then ΔxΔλ~λ2/2π
Okay.. at least with this one I know where it's from.
Ultimately I think what explains why I'm confused is when the book gives an example...
Standing in a 20m long pier, you notice there are always 15 wave crests between the two ends of the pier.
Estimate the minimum uncertainty in the wavelength that could be computed.
Apparently it's 1cm.Huh...?
How does that even work?
I actually don't really get this. Just take a ruler and find the wavelength, what's the pier got to do with it? I understand that the more distance you have the better your accuracy but the big issue is that I don't even accept the existence of the equation which is used, ΔxΔλ because the book just pulled pulled some black magic and tossed this at me.
Ultimately I don't see how there is any "uncertainty" at all. I mean... just look at figure 1, where's the uncertainty? It looks pretty defined to me. I understand that I'm wrong, since this is just all fact but I'm struggling to justify the book's explanations. I'm doing my best to NOT just memorize equations and toss them out on exams.
So I'm just hoping that by giving lots of examples of why I'm confused it's helpful to you guys for understanding what the hell is confusing me, since I don't even know.
Please explain this to me or suggest some sources which could help.
Thanks.
Last edited: