- #1
- 8,221
- 1,944
I am starting this thread to focus on a point discussed in a QP thread. The relevant experiment is referenced below, which is a very complex experiment intending to remove some of the "loopholes" in Bell tests. For this thread, those loopholes don't matter and we won't reference that element. What matters is that entanglement is demonstrated (S=2.4 for CHSH calculation). The entanglement is created by a "traditional" Bell State Measurement (BSM) performed on 2 photons, whose near-simultaneous arrival heralds a psi- state (maximal entanglement, with opposite polarizations) for the pair used for the Bell test. Importantly in this experiment, the BSM (at location C) occurs AFTER the entangled pairs are recorded (at locations A and B)
https://arxiv.org/pdf/1508.05949.pdf
Experimental loophole-free violation of a Bell inequality using entangled electron spins separated by 1.3 km
Hensen et al, 2015.
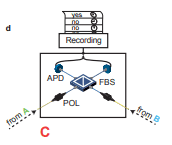
I. The question being posed is as follows: Is Entanglement Swapping a result of a) Post-Selection, or b) a result of the BSM operation? In other words: is swapping a) simply identifying photon pairs that will demonstrate entanglement; or b) is swapping a result of a physical quantum interaction? Here are two opposing interpretations (reference Figure 1):
@vanhees71 takes position a): "If I understand it right, the point is to use entanglement swapping to select (or post-select, which doesn't really matter, if QT is correct, and there's no reason to doubt it, including the result of this experiment!) entangled electron pairs. Without this selection the electron pairs are not entangled at all!"
I say: b) Only a physical operation, performed after the fact, causes the entanglement swap to occur in this experiment. This is a demonstration of quantum nonlocality, which defies the normal cause-effect nature of classical physics. (Note that there is no possibility of sending an FTL signal here. Also note that if you are a fan of "acausal" interpretations, then my position is nothing special.)
Obviously, there are answers provided by various interpretations. But is there an experimental way to discern between a) and b)? Maybe there is. Here is my shot. a) and b) agree that a successful swap occurs when the following criteria are met (as they are in the experiment):
i) A polarized photon from location A and a similarly polarized photon from location B pass through a beam splitter (FBS), and emerge on opposite output ports. Both are transmitted, or both are reflected.
ii) The photons cause the both of the detectors positioned outside the output ports to click simultaneously, where simultaneously is defined as being within a suitably small time window (perhaps on the order of 10 to 50 nanoseconds).
iii) Either the A photon was reflected to the "left" detector and the B photon was reflected to the "right" detector; exclusive or (XOR)
iv) The A photon was transmitted to the "right" detector and the B photon was transmitted to the "left" detector.
In the a) interpretation championed by vanhees71: the above are apparently the only requirements. All that occurs is that we are post-selecting a group that comes along about once an hour. There is no quantum interaction that occurs that defies local causality. There is no expectation that the photon from A has any kind of quantum interaction with the photon from B that is a requirement for identifying an entanglement swap.
In the b) interpretation championed by me DrChinese: there is an additional requirement v), namely that it must not be possible to determine the source of the photon arriving at the "left" detector (which of course would immediately tell us the source of the photon arriving at the "right" detector). This indistinguishability requirement is physical, and is only satisfied when the physical setup does not allow the iii) and the iv) to be distinguished.
Now I'm sure the a) proponents would agree that v) is one of their requirements too, but why? Imagine this scenario, we'll call Alt-BSM. In the Alt-BSM setup, requirements i) ii) iii) and iv) are met - but NOT requirement v) physical indistinguishability. Here is how we will create this. The photons from location A and the photons from location B will be routed to separate but otherwise identical BSM setups. We will record the results and make note of the pairs that meet the requirements of i) ii) iii) and iv) above. We still expect the both to be reflected, or both to be transmitted. We still expect them to arrive simultaneously (within the small time window). However, we will always know which photon comes from the A location, and which comes from the B location, and they will have never had a chance to interact. So the v) requirement (physical interaction) is definitely NOT met. Nonetheless, we will have otherwise satisfied the requirements needed for those who say that the post-selection process merely reveals the small proportion (1 per hour) of pairs in which entanglement had occurred (since the A & B outcomes are recorded before the C outcomes). On the other hand, I say the related A/B pairs will NOT violate a Bell inequality and will have an S value below 2. Thus proving that the v) requirement of physical indistinguishability is essential, and that the only reasonable interpretation is the b) position: the BSM performs a physical operation (entanglement swapping), which violates local causality.
II. Now I know that my friends the a) advocates will kick and scream at my characterization of v), but here is my final proof (actually not a proof, but an experimentally testable question which should provide proof). We already know that the rate of coincidences in the actual experiment are 245 in a 220 hour run. Let's call that 1 per hour. If a) is correct, then if we perform the Alt-BSM version we must get a lot more than 1 qualifying event per hour. Perhaps we would get 3 per hour: 1 of which (a subset) would have also satisfied the actual BSM criteria (thus "post-selecting" the entangled pairings), and maybe a 2 more that would NOT have met the more restrictive criteria (no entanglement). This would demonstrate that only those events in which v) is satisfied are those in which entanglement occurs. On the other hand, if the rate of coincidence remains at about 1 per hour: then we know for a fact that the BSM is a physical operation that violates local causality when it is performed after entangled A and B are detected (as in this experiment). For a) to be valid, there must be a difference in the rate between the performed BSM experiment and my hypothetical Alt-BSM experiment.
So my question to experimenters: run the Hensen et al experiment in the Alt-BSM mode, and tell us the rate of seeing qualifying events. And while you are at it: whether the S value indicates entanglement (S=2.42+/-), no entanglement, or some entanglement. Thoughts?
https://arxiv.org/pdf/1508.05949.pdf
Experimental loophole-free violation of a Bell inequality using entangled electron spins separated by 1.3 km
Hensen et al, 2015.
I. The question being posed is as follows: Is Entanglement Swapping a result of a) Post-Selection, or b) a result of the BSM operation? In other words: is swapping a) simply identifying photon pairs that will demonstrate entanglement; or b) is swapping a result of a physical quantum interaction? Here are two opposing interpretations (reference Figure 1):
@vanhees71 takes position a): "If I understand it right, the point is to use entanglement swapping to select (or post-select, which doesn't really matter, if QT is correct, and there's no reason to doubt it, including the result of this experiment!) entangled electron pairs. Without this selection the electron pairs are not entangled at all!"
I say: b) Only a physical operation, performed after the fact, causes the entanglement swap to occur in this experiment. This is a demonstration of quantum nonlocality, which defies the normal cause-effect nature of classical physics. (Note that there is no possibility of sending an FTL signal here. Also note that if you are a fan of "acausal" interpretations, then my position is nothing special.)
Obviously, there are answers provided by various interpretations. But is there an experimental way to discern between a) and b)? Maybe there is. Here is my shot. a) and b) agree that a successful swap occurs when the following criteria are met (as they are in the experiment):
i) A polarized photon from location A and a similarly polarized photon from location B pass through a beam splitter (FBS), and emerge on opposite output ports. Both are transmitted, or both are reflected.
ii) The photons cause the both of the detectors positioned outside the output ports to click simultaneously, where simultaneously is defined as being within a suitably small time window (perhaps on the order of 10 to 50 nanoseconds).
iii) Either the A photon was reflected to the "left" detector and the B photon was reflected to the "right" detector; exclusive or (XOR)
iv) The A photon was transmitted to the "right" detector and the B photon was transmitted to the "left" detector.
In the a) interpretation championed by vanhees71: the above are apparently the only requirements. All that occurs is that we are post-selecting a group that comes along about once an hour. There is no quantum interaction that occurs that defies local causality. There is no expectation that the photon from A has any kind of quantum interaction with the photon from B that is a requirement for identifying an entanglement swap.
In the b) interpretation championed by me DrChinese: there is an additional requirement v), namely that it must not be possible to determine the source of the photon arriving at the "left" detector (which of course would immediately tell us the source of the photon arriving at the "right" detector). This indistinguishability requirement is physical, and is only satisfied when the physical setup does not allow the iii) and the iv) to be distinguished.
Now I'm sure the a) proponents would agree that v) is one of their requirements too, but why? Imagine this scenario, we'll call Alt-BSM. In the Alt-BSM setup, requirements i) ii) iii) and iv) are met - but NOT requirement v) physical indistinguishability. Here is how we will create this. The photons from location A and the photons from location B will be routed to separate but otherwise identical BSM setups. We will record the results and make note of the pairs that meet the requirements of i) ii) iii) and iv) above. We still expect the both to be reflected, or both to be transmitted. We still expect them to arrive simultaneously (within the small time window). However, we will always know which photon comes from the A location, and which comes from the B location, and they will have never had a chance to interact. So the v) requirement (physical interaction) is definitely NOT met. Nonetheless, we will have otherwise satisfied the requirements needed for those who say that the post-selection process merely reveals the small proportion (1 per hour) of pairs in which entanglement had occurred (since the A & B outcomes are recorded before the C outcomes). On the other hand, I say the related A/B pairs will NOT violate a Bell inequality and will have an S value below 2. Thus proving that the v) requirement of physical indistinguishability is essential, and that the only reasonable interpretation is the b) position: the BSM performs a physical operation (entanglement swapping), which violates local causality.
II. Now I know that my friends the a) advocates will kick and scream at my characterization of v), but here is my final proof (actually not a proof, but an experimentally testable question which should provide proof). We already know that the rate of coincidences in the actual experiment are 245 in a 220 hour run. Let's call that 1 per hour. If a) is correct, then if we perform the Alt-BSM version we must get a lot more than 1 qualifying event per hour. Perhaps we would get 3 per hour: 1 of which (a subset) would have also satisfied the actual BSM criteria (thus "post-selecting" the entangled pairings), and maybe a 2 more that would NOT have met the more restrictive criteria (no entanglement). This would demonstrate that only those events in which v) is satisfied are those in which entanglement occurs. On the other hand, if the rate of coincidence remains at about 1 per hour: then we know for a fact that the BSM is a physical operation that violates local causality when it is performed after entangled A and B are detected (as in this experiment). For a) to be valid, there must be a difference in the rate between the performed BSM experiment and my hypothetical Alt-BSM experiment.
So my question to experimenters: run the Hensen et al experiment in the Alt-BSM mode, and tell us the rate of seeing qualifying events. And while you are at it: whether the S value indicates entanglement (S=2.42+/-), no entanglement, or some entanglement. Thoughts?
Last edited: