Exploring Entanglement Through Laser Light Mixing Experiments

[James2018]

TL;DR Summary

How do these unusual entanglement experiments work?

https://quantum.phys.lsu.edu/old-website/seminars/abstracts/Kaushik10.pdf

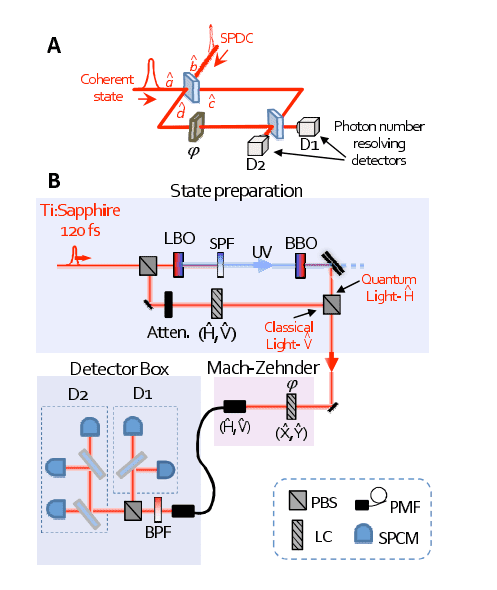
I have discovered an experiment in the link above where you get NOON entangled states by mixing classical laser light with quantum light from SPDC. But I cannot understand the mathematics behind it. Can you explain it to me please?Also, in this experiment they seem to swap the entanglement between mirror and reflected light created by radiation pressure with entanglement between mirrors by interfering light reflected by mirrors?https://arxiv.org/pdf/1508.06462.pdf

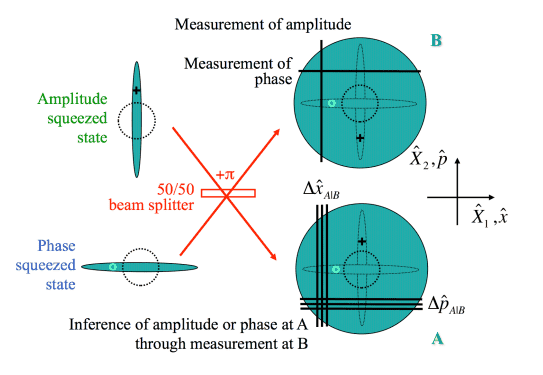
"When two squeezed input fields (here without coherent displacement) are superposed on a (balanced) beam splitter, the two output fields individually show a rather large thermal uncertainty area, and are entangled"Then in the same experiment, they say they obtain a state entangled in phase and amplitude by interfering amplitude squeezed light with phase squeezed light, and that the stronger the input squeezing, the stronger the output entanglement. How does that work?

 

[tade]

the stronger the input squeezing, the stronger the output entanglement.

where do they say that

 

[PeterDonis]

classical laser light

There is no such thing. If classical electrodynamics were correct, lasers would not exist. Lasers are quantum phenomena.

 

[James2018]

where do they say that

Figure 1
https://arxiv.org/pdf/1508.06462.pdf

"For infinitely strong input squeezing the uncertainties ∆x_A|B and ∆p_A|B approach zero and thus resemble maximal EPR entanglement and the commutation relation [xA + xB, pA −pB] = 0. Note that in this case the local thermal uncertainties of the systems A and B are of infinite size. "

Also, they say

"From this picture it may be concluded that maximally entangled systems do not have respective physical properties such as individual positions or individual momenta at all. For systems that are less than maximally entangled, this statement needs to be weakened. In this case the uncertainties/variances in the measurement results of their individual properties describe a finite phase space region within which a definition of the observables does not exist."

 

[James2018]

There is no such thing. If classical electrodynamics were correct, lasers would not exist. Lasers are quantum phenomena.

Yes, but they mean light that is not in a state with fixed photon number, lasers are not a Fock state of light. The uncertainty in amplitude for coherent states is equal to their uncertainty in phase.

Quantum light in this article means anti-bunched photon statistics...

 

[James2018]

Anyway, here is another article that has some maths, but still not enough for me to understand

https://www.degruyter.com/document/doi/10.1515/nanoph-2015-0142/html

"Phase space representation of two outputs. (A) Outputs are entangled EPR1 and EPR2 beams when the incident squeezed light beams SL1 and SL2 are combined with relative phase ϕ of 90°. (B) Outputs are two independent squeezed light SL1' and SL2' when the squeezed light beams SL1 and SL2 are combined with ϕ of 0°."

 

[PeterDonis]

they mean light that is not in a state with fixed photon number, lasers are not a Fock state of light. The uncertainty in amplitude for coherent states is equal to their uncertainty in phase.

Quantum light in this article means anti-bunched photon statistics...

To me this just means the article is using bad terminology. As I said, lasers can't even exist under classical electrodynamics.

As far as I can tell, this bad terminology doesn't actually contribute anything to the reasoning in the article, so it's not doing a lot of damage, but that still doesn't make it a good idea IMO.

 

[Cthugha]

There is no such thing. If classical electrodynamics were correct, lasers would not exist. Lasers are quantum phenomena.

The definition of "what is non-classical" is a nontrivial one, but the standard definition in the discrete variable quantum optics community is that intensity fluctuations below shot noise make light fields non-classical which is technically described by the equal-time second-order photon correlation function taking on values lower than one. Figuratively speaking, this means that the conditional probability to detect another photon based on the information that one photon was detected right now, will be reduced. For some other strongly fluctuating light fields, this probability will be enhanced. For coherent light fields, this probability does not change at all, so a measurement that destroys a photon does not change the conditional expectation values of the mean intensity and similar quantities. This is the closest thing to having a non-invasive measurement which you can get to in standard experiments with detectors based on absorption and accordingly laser light is commonly referred to as the most classical light there is. Calling laser light classical is standard terminology.

With respect to whether lasers are intrinsically quantum: Willis Lamb wrote a paper exactly on this topic:
https://journals.aps.org/pra/abstract/10.1103/PhysRevA.5.1298

Unless you go to single atom lasers or cavity QED, non-quantum physics is sufficient to describe most aspects of laser physics for, e.g., free electron lasers (unless you go to very short wavelengths) or lasers based on continuous active media such as plasmas. However, there are of course plenty of lasers where you need quantum mechanics already to describe the emitter acting as the active medium properly, e.g., for atoms.

Irrespective of that, it is of course very reasonable to perform a quantum treatment in all cases.

 

[PeterDonis]

non-quantum physics is sufficient to describe most aspects of laser physics for, e.g., free electron lasers (unless you go to very short wavelengths) or lasers based on continuous active media such as plasmas

I can't read the Lamb paper because it's behind a paywall. The main obstacles I see are explaining the existence of atoms classically in the first place (which many "classical" treatments gloss over, but I don't think that's right--in classical physics atoms can't exist), and explaining stimulated emission classically.

Would it be reasonable to say that in this context, "classical" and "non-classical" are purely technical terms in quantum optics, where "classical" does not mean a treatment that purely relies on classical (pre-quantum) physics, but instead is a more "semi-classical" treatment where some classical equations are used as approximations but it is acknowledged that quantum physics is needed to ultimately explain what is going on (for example, because atoms can't exist otherwise)?

 

[vanhees71]

"Semiclassical approximation" usually means you treat the charged particles quantum theoretically and the em. field as classical c-number field. You get pretty far with this approximation. E.g., the usual leading-order results in QED perturbation theory for the Compton effect or the photoelectric effect were obtained first in this approximation. The most simple examples that can't be described in this way is spontaneous emission, "quantum beats", and the HOM experiment.

 

[Cthugha]

I can't read the Lamb paper because it's behind a paywall. The main obstacles I see are explaining the existence of atoms classically in the first place (which many "classical" treatments gloss over, but I don't think that's right--in classical physics atoms can't exist), and explaining stimulated emission classically.

Would it be reasonable to say that in this context, "classical" and "non-classical" are purely technical terms in quantum optics, where "classical" does not mean a treatment that purely relies on classical (pre-quantum) physics, but instead is a more "semi-classical" treatment where some classical equations are used as approximations but it is acknowledged that quantum physics is needed to ultimately explain what is going on (for example, because atoms can't exist otherwise)?

I fully agree that you need QM to explain atoms. You just do not necessarily need atoms to build a laser. Free electron lasers or many semiconductor diode lasers work quite differently.

I also agree that "classical" and "non-classical" are technical terms in quantum optics. Nowadays, quantifying this non-classicality and finding suitable quantifiers has become a research direction of its own. Typically, the term is understood to refer to light fields that cannot be described by classical electromagnetism. It aims rather at the properties of the light field itself, not at the way the light fields were created.
The most commonly encountered non-classical light fields are in my opinion light fields with sub-Poissonian noise statistics (e.g., Fock states) in discrete variable quantum optics and squeezed light fields in continuous variable quantum optics. Typical non-classicality identifiers would then be a value of g(2)(0) that goes below 1, a Wigner function showing negative values, quadrature noise below the shot-noise limit and so on.

 

[PeterDonis]

Free electron lasers

Hm, yes, a purely classical explanation might work for those.

or many semiconductor diode lasers work quite differently.

Diodes are solids and classical physics has the same problem explaining those as it does explaining atoms.

I also agree that "classical" and "non-classical" are technical terms in quantum optics. Nowadays, quantifying this non-classicality and finding suitable quantifiers has become a research direction of its own. Typically, the term is understood to refer to light fields that cannot be described by classical electromagnetism. It aims rather at the properties of the light field itself, not at the way the light fields were created.

Thanks, this is good background.

 

[Cthugha]

Diodes are solids and classical physics has the same problem explaining those as it does explaining atoms.

To some degree: yes. There are solid state lasers such as Nd:YAG, where that is certainly the case.
Some semiconductor diode lasers, especially the ones which are widely tunable, instead work on the principle that the material is simply flooded with electrons and holes and lasing occurs from this electron-hole plasma which can be approximated reasonably well within a classical picture.

Of course, there is always the question of how far down the rabbit hole one wants to go. If you want to describe why conduction and valence bands exist in the first place, you of course need to go back to quantum mechanics.

 

[PeterDonis]

If you want to describe why conduction and valence bands exist in the first place, you of course need to go back to quantum mechanics.

Yes, that was my point about solids. I understand that, for certain problems, if you take the existence of these bands as given, the rest of the analysis can be classical (just as, for certain problems, if you take the existence of atoms as given, the rest of the analysis can be classical).

 

[Cthugha]

Anyway, here is another article that has some maths, but still not enough for me to understand

https://www.degruyter.com/document/doi/10.1515/nanoph-2015-0142/html

It is a bit difficult to suggest a better introduction without knowing about your background.
This review article from the Review of Modern Physics provides a reasonably pedagogical introduction:
https://arxiv.org/pdf/quant-ph/0410100.pdf

The introduction to what continuous variable entanglement is and what the states should look like in general is given on the first 15 to 20 pages and the discussion on how to implement such states experimentally starts on page 53.

 

[vanhees71]

This would be a very nice paper, if they'd not use the idiosyncratic choice of natural units setting $\hbar=1/2$ (sic!). That drives me nuts, figuring out where all these factors 2 come from...

 

[Cthugha]

Well, yes, that is the standard problem in the field. Of course they do not really set $\hbar=1/2$, but the question is what people prefer the quadratures to behave like. Some people want them to behave exactly like position and momentum, while others want them to correspond to the fields. People usually just choose the convention that requires them to include fewer factors of 2 in their further calculations.

Actually, my students also frequently wasted quite some time on that and now routinely define the quadratures as $\hat{q}=A(\hat{a}^\dagger +\hat{a})$ and $\hat{p}=A i(\hat{a}^\dagger -\hat{a})$, the commutation relation as $[\hat{q},\hat{p}]=2A^2 i$, the uncertainty product $\Delta q \Delta p\leq A^2$ and the photon number as $\langle n \rangle=\frac{1}{4 A^2}(\langle \hat{q}^2 \rangle +\langle \hat{p}^2\rangle)-\frac{1}{2}$ and then just pick A according to whatever paper they refer to at the moment.