Exploring k-Equivalence in Computability Theory

[evinda]

Hello! (Wave)

In the notes of computability theory, I found the following:

$$q \sim_0 q' (\text{ q, q' are 0-equivalent}) \Leftrightarrow \text{For each input, q,q' have the same output} $$

$$q \sim_k q' (\text{ q, q' are k-equivalent}) \Leftrightarrow \text{ q,q'are 0-equivalent and } \forall x \in \Sigma , \delta(q,x) \sim_{k-1} \delta(q',x)$$

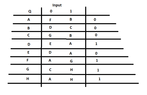
We have the following:

View attachment 5802

$0$-equivalent: $\{ A,B,C,E\}, \{ D,F,G,H\}$

$1$-equivalnt: $\{ A,B,C,E\}, \{D\}, \{ F,G,H\}$

$2$-equivalent: $\{A,C\}, \{B,E\}, \{ D \}, \{ F,G,H\}$

$3$-equivalent: $\{A,C\}, \{B,E\}, \{ D \}, \{F,G,H \}$

Could you explain to me how we found the $k$-equivalent sets for $k \geq 1$ ?
How do we find the states $q, q'$ for which $\delta(q, x) \sim_{k-1} \delta(q',x)$ ?

 

[Evgeny.Makarov]

What kind of finite automata are you talking about? What do the columns of the table mean?

 

[evinda]

What kind of finite automata are you talking about? What do the columns of the table mean?

Machines of finite states are meant. At the first column we have the states. At the two next columns we have the transitions and at the fourth column we have the output.

 

[Evgeny.Makarov]

Machines of finite states are meant.

Have you encountered infinite states somewhere? (Smile)

At the first column we have the states. At the two next columns we have the transitions and at the fourth column we have the output.

So the output depends only on the state and not on the input? I have not seen such automata before. It may be good to provide a definition in order to be sure.

 

[I like Serena]

Could you explain to me how we found the $k$-equivalent sets for $k \geq 1$ ?
How do we find the states $q, q'$ for which $\delta(q, x) \sim_{k-1} \delta(q',x)$ ?

Machines of finite states are meant. At the first column we have the states. At the two next columns we have the transitions and at the fourth column we have the output.

States $q$ and $q'$ are considered 1-equivalent if both $\delta(q,0) \sim_0 \delta(q',0)$ and $\delta(q,1) \sim_0 \delta(q',1)$.

Let's take a look at $A$ and $B$.
We have $\delta(A,0)=F$ and $\delta(B,0)=D$.
We've already found that $F$ and $D$ are 0-equivalent, so $\delta(A,0) \sim_0 \delta(B,0)$.
Same for $\delta(A,1)=B \sim_0 C=\delta(B,1)$.
So $A \sim_1 B$.

Are $A$ and $C$ 1-equivalent?
And $D$ and $F$?
How about whether $A$ and $B$ are 2-equivalent?

 

[evinda]

Have you encountered infinite states somewhere? (Smile)

No, I haven't seen them.
Machines of finite states is the titel of the chapter where I found the $k$-equivalent states.

So the output depends only on the state and not on the input? I have not seen such automata before. It may be good to provide a definition in order to be sure.

I have the definition that I wrote at my initial post.

 

[evinda]

States $q$ and $q'$ are considered 1-equivalent if both $\delta(q,0) \sim_0 \delta(q',0)$ and $\delta(q,1) \sim_0 \delta(q',1)$.

Let's take a look at $A$ and $B$.
We have $\delta(A,0)=F$ and $\delta(B,0)=D$.
We've already found that $F$ and $D$ are 0-equivalent, so $\delta(A,0) \sim_0 \delta(B,0)$.
Same for $\delta(A,1)=B \sim_0 C=\delta(B,1)$.
So $A \sim_1 B$.

Are $A$ and $C$ 1-equivalent?
And $D$ and $F$?
How about whether $A$ and $B$ are 2-equivalent?

We have that $\delta(A,0)=F$ and $\delta(C,0)=G$ and we know that $F \sim_0 G$. Also we have that $\delta(A,1)=B \sim_0 \delta(C,1)=B$.

So $A \sim_1 C$.

$\delta(D,0)=E \not\sim_0 \delta(F,0)=A$.

So $D$ and $F$ are not 1-equivalent.

$A$ and $B$ are not $2$-equivalent since $\delta(A,0) \not\sim_1 \delta(B,0)=D$.

We get the same set of states to be $2$- and $3$- equivalent.

Will the same sets be $k$-equivalent for any $k \geq 4$ ?

 

[Evgeny.Makarov]

No, I haven't seen them.
Machines of finite states is the titel of the chapter where I found the $k$-equivalent states.

My reply was supposed to underscore a funny interpretation of the phrase "Machines of finite states". On the surface this may mean "machines consisting of finite states". I have never seen the concept of a "finite state" (as a noun) in the theory of computation. What people study are machines with finite or infinite number of states. Thus, it's the set of states in a machine and not states themselves that can be finite or infinite. The phrase "finite-state" is used as an adjective rather than as a noun. Correspondingly, I was hoping you would rewrite "machines of finite states" as "machines with finite number of states".

I have the definition that I wrote at my initial post.

I mean the definition of the type of machines, not this particular machine. Something like "a finite automaton is a quintuple $(Q,\Sigma,\delta,q_0,F)$..." Otherwise there is a lack of clarity in the problem statement. For example, as I understand, ILS started answering without taking outputs into account at all.

 

[I like Serena]

It appears we can solve the problem without actually knowing what these outputs connected to states are, especially since evinda only asked for help when $k\ge 1$.
Those output states might mean anything. I'd like to interpret them as final states, which makes sense. Maybe it was something that got lost in translation? (Wondering)

 

[Evgeny.Makarov]

The definition of $\sim_k$ is similar to that in Lewis, Papadimitriou, pp. 98-99, but not exactly the same.

 

[I like Serena]

The definition of $\sim_k$ is similar to that in Lewis, Papadimitriou, pp. 98-99, but not exactly the same.

What is the difference?

Will the same sets be $k$-equivalent for any $k \geq 4$ ?

Yes.
Since it didn't change in the last iteration, it won't change in another iteration. (Nod)

 

[Evgeny.Makarov]

What is the difference?

In L&P we say that $q\sim_k p$ if $q\sim_{k-1} p$ and $\delta(q,a)\sim_{k-1}\delta(p,a)$ for all $a\in\Sigma$. In fact, this is an equivalent characterization, and the original definition is that $q\sim_k p$ if $\delta(q,w)\in F\iff\delta(p,w)\in F$ for all $w\in\Sigma^*$ such that $|w|\le k$. This is for conventional DFAs, without any output.