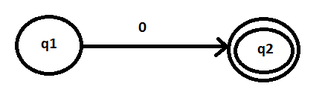- #1
evinda
Gold Member
MHB
- 3,836
- 0
Hello! (Wave)
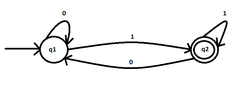
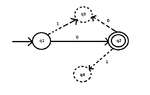
The following DFA is given:
View attachment 5685
I want to find the language that it recognizes. The alphabet is $\Sigma=\{0,1\}$.
Isn't the language this one: $(0^{\ast} 1^{+} 0^{\ast} )^{+}$?
Also I want to draw a dfa that recognizes the following languages and that have the referred number of states. The alphabet is still $\{0,1\}$.
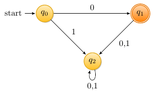
But can it be that $1$ goes nowhere?
But then the word $1$ isn't accepted... :( What could we change?
Can it be that 0 and 1 go nowhere? (Worried)
Again $1$ goes nowhere... Is that possible?
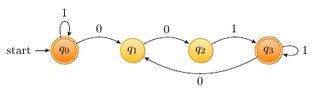
The following DFA is given:
View attachment 5685
I want to find the language that it recognizes. The alphabet is $\Sigma=\{0,1\}$.
Isn't the language this one: $(0^{\ast} 1^{+} 0^{\ast} )^{+}$?
Also I want to draw a dfa that recognizes the following languages and that have the referred number of states. The alphabet is still $\{0,1\}$.
- $\{0\}$, with two states
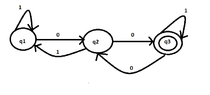
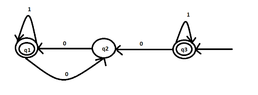
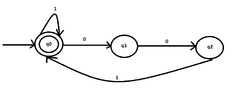
- $1^{\ast} (001^+)^{\ast}$, with 3 states
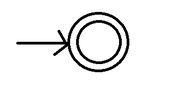
- $\{ \epsilon \}$ , with 1 state
- $0^{\ast}$ with 1 state
But can it be that $1$ goes nowhere?
But then the word $1$ isn't accepted... :( What could we change?
Can it be that 0 and 1 go nowhere? (Worried)
Again $1$ goes nowhere... Is that possible?