- #1
How Does Linkage Motion Affect Rotation and Yaw in 3D Space?
In summary, the article examines the mechanics of link movement in a three-dimensional space, specifically focusing on the rotation and yaw of a linkage system. It discusses the principles governing the movement along the X, Y, and Z axes, detailing how different forces and angles affect the linkage's orientation and stability. The exploration aims to enhance the understanding of mechanical linkages in various applications, such as robotics and engineering designs.
- #2
sophiecentaur
Science Advisor
Gold Member
- 29,678
- 7,212
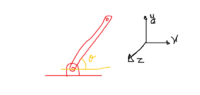
Is your question about the use of the word "yaw"? This will happen if the bottom hinge cheeks do not fit exactly. You need to be "clear" first.Micheal_Leo said:
Lateral movement of the link can be parallel with the z axis or at an angle (tipping). Are you looking for a way to specify what you need?
- #3
Micheal_Leo
- 79
- 4
sophiecentaur said:Is your question about the use of the word "yaw"? This will happen if the bottom hinge cheeks do not fit exactly. You need to be "clear" first.
Lateral movement of the link can be parallel with the z axis or at an angle (tipping). Are you looking for a way to specify what you need?
the link has pin joint with bracket which fixed and also link move back and forth, so i am trying to fugure out that motion and angle how this link will make in the 3d axis i mention it
Last edited:
- #4
sophiecentaur
Science Advisor
Gold Member
- 29,678
- 7,212
It depends on how good you make the hinge arrangement, surely. The rod can move laterally or rotate about the z axis. Is that not obvious? Motion can be limited by having a long enough bearing and pin and / ormaking sure that the D shaped bracket in your picture is big enough and tight enough on the rod. You have not specified the actual dimensions so how can I answer your question? In fact you haven't actually asked a questionMicheal_Leo said:
I asked you why you used the word "yaw". You could add the word "rotation"but you need more (3D) details on your sketch. The rod can rotate about its axis (twist) as well as from side to side.