Exploring Photon Mass: Is It Zero or Relativistic?

[Garlic]

Hello everyone,
I know that the photon has zero rest mass and I know that otherwise the relativistic mass formula would not make sense.

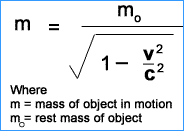
When I searched for an answer to the question "how can a particle have zero mass and still possesses energy if E=mc^2" I got an answer saying the mass energy relation formula is actually E= m^2 c^4 times p^2 c^2 when we talk about a non massive particle. Back then I diddn't think about p=mv formula has a mass in it.

The problem started when our physics teacher argued that although photons doesn't have rest mass, they still have a relativistic mass. We transformed these formulas E=mc^2 and E=hf to give us the photon mass m=h/λc. The teacher also said that the photons have momentum, and we can see it in the deflection of the halley comet near the sun, and that we can even build a solar sail that uses the momentum of the photons (he diddn't mean solar cells).

So my knowledge about photon mass is contradicting with itself. Where am I wrong?

 

[jbriggs444]

I know that the photon has zero rest mass and I know that otherwise the relativistic mass formula would not make sense.

Relativistic mass is not a concept that is taught much these days. It is not needed and confuses more than it explains.

When I searched for an answer to the question "how can a particle have zero mass and still possesses energy if E=mc^2" I got an answer saying the mass energy relation formula is actually E= m^2 c^4 times p^2 c^2 when we talk about a non massive particle

That formula holds for both massive particles and those without mass. Except it's $E^2 = m^2c^4 + p^2c^2$

Back then I diddn't think about p=mv formula has a mass in it.

The formula for the momentum of a massive particle expressed in terms of the particle's mass and velocity is $p = \frac{mv}{\sqrt{1-\frac{v^2}{c^2}}}$. The m there is the particle's rest mass. For low speed objects, this reduces to the familiar p=mv. For relativistic speeds, the factor of gamma is still there, but it is not tied to the mass term.

The problem started when our physics teacher argued that although photons doesn't have rest mass, they still have a relativistic mass. We transformed these formulas E=mc^2 and E=hf to give us the photon mass m=h/λc.

That gives you the photon's relativistic mass. But again, "relativistic mass" is not a concept that is used much any more. The term "mass" by itself means rest mass these days.

The teacher also said that the photons have momentum, and we can see it in the deflection of the halley comet near the sun, and that we can even build a solar sail that uses the momentum of the photons (he diddn't mean solar cells).

So my knowledge about photon mass is contradicting with itself. Where am I wrong?

If you want the momentum of a particle that is massless then the $E^2 = m^2c^4 + p^2c^2$ formula can help you. You know the photon's energy by $E=h\nu$. You may know that the photon's rest mass (or, more properly, its "invariant mass") is zero. So the photon's momentum is $p^2c^2 = E^2$ so $p=\frac{E}{c}=\frac{h\nu}{c}$

 

[Garlic]

But again, "relativistic mass" is not a concept that is used much any more.

But why? Relativistic mass is something concrete, when the relativistic mass of an electron in a system increases, basically the observed mass of the electron will increase. This couldn't be explained without relativistic mass concept.

And then there is this question about gravitational lensing: do the photons get deflected because of their relativistic masses, or because the spacetime gets deflected because of the huge mass and photons are actually going in a straight path?

 

[jbriggs444]

But why? Relativistic mass is something concrete, when the relativistic mass of an electron in a system increases, basically the observed mass of the electron will increase. This couldn't be explained without relativistic mass concept.

Yes, the observed energy of the electron increases. But relativistic mass is given by $m_{rel}=E/c$. High energy physics is often done using a system of units in which c=1. Energy and relativistic mass are the same thing. There is no point having two names for the same thing. So the notion of energy was retained and the notion of relativistic mass was discarded.

And then there is this question about gravitational lensing: do the photons get deflected because of their relativistic masses, or because the spacetime gets deflected because of the huge mass and photons are actually going in a straight path?

Photons do not get deflected. They follow straight line paths (also known as geodesics). It is space-time that is curved. The curvature of space time is determined by the stress-energy tensor, not just by the presence of mass.

 

[Nugatory]

But why? Relativistic mass is something concrete, when the relativistic mass of an electron in a system increases, basically the observed mass of the electron will increase. This couldn't be explained without relativistic mass concept.

Just how concrete is this mass increase? You can't plug the relativistic mass into $F=ma$ to get the acceleration caused by a given force - the same force produces different accelerations when applied in different directions relative to the direction of motion. You can't plug it into $E_k=mv^2/2$ to get the kinetic energy - that's $(m_r-m_0)c^2$. You can't plug it into $F=Gm_1m_2/r^2$ to get the gravitational force it produces. You can't use it in the formula $R=2Gm/c^2$ to find the radius of the event horizon of a black hole moving relative to you.

So what physical significance does the relativistic mass have? It's convenient when we're applying a force exactly perpendicular to the direction of motion, but that's about the only thing it's good for. Other simplfications, such as writing $E=m_rc^2$ instead of $E^2=(m_0c^2)^2+(pc)^2$ and $p=m_rv$ instead of $p=\gamma{m}_0v$ obscure more than they reveal.

 

[Garlic]

I understand now, thank you.

 

[DrStupid]

You can't plug it into $E_k=mv^2/2$ to get the kinetic energy - that's $(m_r-m_0)c^2$. You can't plug it into $F=Gm_1m_2/r^2$ to get the gravitational force it produces.

You can't do that with rest mass either. Relativistic mass simply got out of fashion. That's it. Don't try to find objective reasons where there are none.

 

[Nugatory]

You can't do that with rest mass either.

Why not? Try it and you'll get classical mechanics, an approximation so good that for several centuries it was believed to be exact. It may be that relativistic mass "got out of fashion", but if so this is one of the situations where fashion was driven by utility.

 

[klotza]

I wrote an article touching on it, klotza.blogspot.com/2015/08/what-heeck-how-stable-is-photon.html

 

[DrStupid]

Why not?

Because it is even worse than using the relativistic mass instead.

It may be that relativistic mass "got out of fashion", but if so this is one of the situations where fashion was driven by utility.

That's a matter of opinion.

 

[Dale]

It may be that relativistic mass "got out of fashion", but if so this is one of the situations where fashion was driven by utility.

I agree.

The timelike component of the four momentum is a useful concept. The norm of the four momentum is also a useful concept. All words are, in some sense, a fashion. Adopting a fashion that assigns different short names to both is indeed a useful fashion. Far more useful (IMO) than assigning two short names to one concept and none to the other.

 

[Oly]

Photons do not get deflected. They follow straight line paths (also known as geodesics). It is space-time that is curved. The curvature of space time is determined by the stress-energy tensor, not just by the presence of mass.[/QUOTE]

OK, I've been hearing this for over a half-century; that space time is curved by the presence of mass and the result is what we call "Gravity".

And what, exactly, causes the curvature?

If the presence of mass causes it, it seems to be "gravity" causes curvature, causes "Gravity" - a circular argument.

-Oly

 

[Dale]

And what, exactly, causes the curvature?

The stress energy tensor:
https://en.m.wikipedia.org/wiki/Einstein_field_equations

 

[PeterDonis]

space time is curved by the presence of mass

You appear to be interpreting this as "spacetime curvature is the same as the presence of mass", but what physicists actually mean by it is "spacetime curvature is caused by the presence of mass" (or more precisely by the stress-energy tensor, which includes mass/energy density but also includes other things).

And what, exactly, causes the curvature?

See above.

 

[echaniot]

Actually, on relativistic mass you can think of it this way:

The total energy of a point mass in motion can be given by the formula:
E = T + mc**2
In case u <<c , E = 1/2 * mu**2 + mc**2 (1)
T_cl = 1/2 * mu**2

while,

when u->c, E = (γ-1)*mc**2 + mc**2 (2)
T_rel = (γ-1)*mc**2
with γ = 1/sqrt(1- (u/c)**2)
(This is relativistic mechanics- the way the universe behaves near the speed of light)

Do not think for a moment about relativistic mass. The m here, is the energy measured in a reference frame in which the particle is at rest.
What is the difference between the two equations (1) and (2)?

Take eqn.(1) and differentiate the kinetic energy with respect to velocity.
You will find: dT_cl/T_cl = 2 *du/u (1.A)

Do the same for eqn.(2): (a bit more tricky):
If I have calculated correctly: dT_rel/T_rel = [(γ**3 * (u/c)**2)/(γ-1)]*du/u (2.A)

What do the two equations tell us?
In the classical case, (1.A), if you increase the particle's kinetic energy by 10%, the velocity will increase by 5%.
In the relativistic case, (2.A),
suppose γ>>1 and u/c~1 . You will see that dT/T~γ**2* du/u. For u = 0.9999c, γ~70 and dT/T = 4.900*du/u.
Thus a 10% increase in kinetic energy implies 0.002% increase in velocity!)


I could add a plot if you consider it helpfulIf you increase the particle's kinetic energy, the increase in velocity will depend on the magnitude of velocity itself. The higher your velocity, the more difficult it will be to increase it . Therefore, it isn't the mass itself that increases. This is a failed and full of misconceptions explanation. It is the mechanics of the universe at high speeds that changes.

Does the photon have mass? No. Why? Because we cannot consider a rest frame for the photon so as to measure its energy at rest and define a value for it. Remember: In photon interactions, we care about energy and momentum. These two are well defined even for massless particles. (E= p.c)
Then what is m=E/c^2?
It is the mass of an object having energy equal to the energy of the photon. Or the mass lost by an object from which the photon was emitted.

 

[DrStupid]

Then what is m=E/c^2?
It is the mass of an object having energy equal to the energy of the photon.

Only if the object is at rest.

 

[echaniot]

@ DrStupid, very much correct. Thanks !

 

[Vijay Vithlani]

Is there any experiment to prove that photon has no mass.
I am saying this because I can prove that " Photon has mass".

 

[jbriggs444]

Is there any experiment to prove that photon has no mass.
I am saying this because I can prove that " Photon has mass".

We all agree that a photon has both momentum and "relativistic mass" in any particular frame of reference. But the word "mass" by itself is taken to mean "invariant mass". Experiment puts a very small limit on how large the invariant mass of a photon could possibly be. The invariant mass of a photon is experimentally indistinguishable from zero.

In general, scientific experiments cannot prove that scientific propositions are true. They can only demonstrate that such propositions are false. If a large number of careful experiments aimed at disproving the consequences of a proposition fail to do so, that tends to confirm the truth of the hypothesis. That is as good as it ever gets.

 

[Vijay Vithlani]

With an experiment I can show photons getting gravitational pull.
What I want to say is I can concentrate light on spot, without using any kind of reflection or refraction.

 

[PeterDonis]

With an experiment I can show photons getting gravitational pull.

This just means photons have energy. It doesn't mean photons have invariant mass.

 

[jtbell]

With an experiment I can show photons getting gravitational pull.

This does not require that the photon have mass.
https://www.physicsforums.com/threads/why-are-massless-photons-affected-by-gravity.511173/

 

[mfb]

The deflection of photons by Earth is about 1 part in a billion. You do not have the equipment to detect any gravitational influence on light, and the gravitational influence of light (on other things) is more than 20 orders of magnitude weaker.

Experimentally, it is not possible to rule out arbitrarily small masses because no measurement is exact, but the upper limit on a photon mass is 10^-18 eV, or 2*10^-54 kg (source). That is a really good upper limit.

 

[Oly]

Some time ago, I posted that if space-time is distorted by the presence of physical mass, and this "curvature of space-time" is then cited as the "cause" of gravity, the argument is circular: Mass distorts spacetime, distorted spacetime causes the 'attraction' called gravity, ergo mass causes gravity.

This generated several hollow replies, so I ask again: If mass has no attraction (which we call "Gravity") - how does mass affect spacetime?

ie: "How many Angels can dance on the point of a pin?"

-Oly

 

[jbriggs444]

Some time ago, I posted that if space-time is distorted by the presence of physical mass, and this "curvature of space-time" is then cited as the "cause" of gravity, the argument is circular: Mass distorts spacetime, distorted spacetime causes the 'attraction' called gravity, ergo mass causes gravity.

The thing that you are arguing against is your own construction and is not even correct. The "distortion" of space-time is not determined by mass. It is determined by the stress-energy tensor. It is not an attraction. It is not caused by gravity. It is gravity.

 

[mfb]

the argument is circular: Mass distorts spacetime, distorted spacetime causes the 'attraction' called gravity, ergo mass causes gravity

There is nothing circular (although you should replace "mass" by "stress-energy tensor"). A causes B, B causes C, therefore A causes C.

 

[Dale]

Some time ago I posted

And you were correctly answered some time ago. The source of gravitation is the stress energy tensor. Nothing circular about it.

 

[Ibix]

Some time ago, I posted that if space-time is distorted by the presence of physical mass, and this "curvature of space-time" is then cited as the "cause" of gravity, the argument is circular: Mass distorts spacetime, distorted spacetime causes the 'attraction' called gravity, ergo mass causes gravity.

As others have noted, mass is not the only source of gravity. The stress energy tensor encodes all sources of gravity, which is a considerably broader range of phenomena than just mass.

This generated several hollow replies, so I ask again: If mass has no attraction (which we call "Gravity") - how does mass affect spacetime?

General relativity describes the curvature correctly to the precision of our measurements. It doesn't explain how it comes about. A future quantum theory of gravity may provide an explanation.