Exploring Proper Time in FLRW Metric: Meaning and Visualization

[Ennio]

TL;DR Summary

If we consider a time variance in FLRW metric, how can we visualize an emitter (having proper time) in the 4D spacetime geometry?

The FLRW metric has been introduced to characterize the homogeneity and isotropy of the Universe and accordingly to obtain "easy" manageable solutions in Friedmann equations.

The FLWR metric is

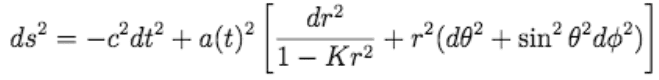
where the LHS can be written as

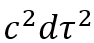where

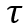is the proper time (despite we know that time is invariant in the formulation).

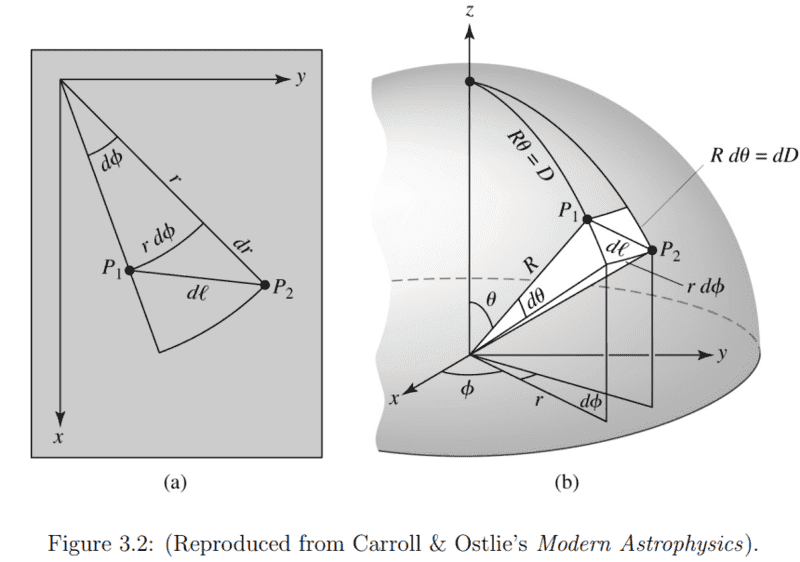
Please refer to the image below to visualize the 4D spacetime geometry used to derive the metric.

My questions is:
Let assume that the we do want to theoretically discuss a time variance in the equation.
In the 4D visualization, where is actually the observer placed? In one of the two spacetime events P1 or P2 ? Not in the center of the geometry.
Accordingly, does the proper time

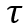refer to an event occurring, for instance, in P2 with respect to the observer, if placed in P1?
In this case, P2 emits the signal which is received by P1.
Am I making a conceptual mistake?

Thank you for supporting me.
E.

 

[Orodruin]

What do you mean by

Let assume that the we do want to theoretically discuss a time variance in the equation.

?

The coordinates are based on an arbitrary point in a spatially homogeneous spacetime. A comoving observer can be taken to have any coordinates.

 

[Ennio]

What do you mean by

?

The coordinates are based on an arbitrary point in a spatially homogeneous spacetime. A comoving observer can be taken to have any coordinates.

I mean that I would like to study a possible difference between cosmic and proper time. Why should time be invariant? Anyway, my question was related to the identification of the emitter in the 4D geometry. Are basically observer and emitter associated to P1 and P2 (see original picture I posted). Thank you!

 

[Ibix]

Let assume that the we do want to theoretically discuss a time variance in the equation.

Do you mean you want to consider a perturbed version of the FLRW spacetime? Making it slightly more realistic so that stars and galaxies could form over time instead of there being a perfectly uniform fluid everywhere in spacetime?

In the 4D visualization, where is actually the observer placed?

Well, the two visualisations are of 2d spatial slices embedded into a (purely invented) 3d space. Accordingly there may be observers at any location. Furthermore, the lines marked $dl$ are spatial displacements, so don't correspond to any interval of proper time at all - they are spacelike paths.

In this case, P2 emits the signal which is received by P1.

There are no signals represented in those diagrams.

 

[Orodruin]

I mean that I would like to study a possible difference between cosmic and proper time.

Cosmic time is the proper time of a comoving observer. If an observer moves relative to the comoving frame, they will be time dilated accordingly relative to cosmological time.

Are basically observer and emitter associated to P1 and P2 (see original picture I posted). Thank you!

All points in space are completely equivalent. This is what homogeneity means. You can therefore pick any two points as long as they have the correct comoving distance between them. Of course, some choices (such as placing emitter or observer at r=0) makes life easier than others.

 

[Ibix]

I mean that I would like to study a possible difference between cosmic and proper time.

Assuming that by "cosmic time" you mean the time coordinate, $t$, this is a completely different thing from proper time, which is the time experienced by any arbitrary observer between two points.

Why should time be invariant?

It isn't, in general. The proper time along a specified path is an invariant, certainly, and (as Orodruin has just noted) the cosmic time is the proper time since the singularity experienced by observers at rest with respect to the matter in the universe.

 

[Dale]

Summary: If we consider a time variance in FLRW metric, how can we visualize an emitter (having proper time) in the 4D spacetime geometry?

In the 4D visualization, where is actually the observer placed? In one of the two spacetime events P1 or P2 ? Not in the center of the geometry.

If there is a particular observer of interest (which is not necessary) then you would typically place them in the center. I am unsure why you would say “not in the center”. The center is arbitrary and any point can be selected as such.