- #1
evinda
Gold Member
MHB
- 3,836
- 0
Hello! (Wave)
According to my notes:
Template algorithm
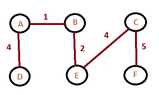
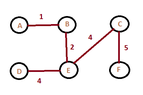
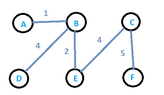
The algorithm keeps the invariant :
"before each iteration,the set $A$ of vertices is a subset of some minimum spanning trees" at each step,where $A$ is an initial set of vertices.
Definition:
The edge $(u,v)$ is called secure for the set $A$,if it can be added to it,without the violation of the invariant.Could you explain me the following sentence? (Thinking)
The algorithm keeps the invariant :
"before each iteration,the set A of vertices is a subset of some minimum spanning trees" at each step,where $A$ is an initial set of vertices.
According to my notes:
Template algorithm
The algorithm keeps the invariant :
"before each iteration,the set $A$ of vertices is a subset of some minimum spanning trees" at each step,where $A$ is an initial set of vertices.
Code:
Template algorithm(G)
A<-∅
while A isn't a connected component
we define an edge (u,v),that is secure for A
A<-A U {(u,v)}
return ADefinition:
The edge $(u,v)$ is called secure for the set $A$,if it can be added to it,without the violation of the invariant.Could you explain me the following sentence? (Thinking)
The algorithm keeps the invariant :
"before each iteration,the set A of vertices is a subset of some minimum spanning trees" at each step,where $A$ is an initial set of vertices.