Exploring the Advantage of Using Pulleys in Two Block Problems

[rudransh verma]

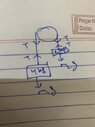
Homework Statement

Two blocks of mass m1=4kg and m2=2kg are hanging in Atwood machine. The total downward trust on the pulley is—

Relevant Equations

$F=ma$

$(T-m1g)-(T-m2g)=(m1+m2)a$
But I think this is wrong eqn.

 

[Doc Al]

Rather than pull an equation from the air, analyze each block separately. Then you can combine the two equations to solve for the tension in the rope.

 

[jbriggs444]

Rather than pull an equation from the air, analyze each block separately. Then you can combine the two equations to solve for the tension in the rope.

Are we not already analyzing exactly the same problem in https://www.physicsforums.com/threads/two-bodies-hanging-from-pulley.1011640/

The two masses there have a different ratio, but it is otherwise the identical situation.

 

[Doc Al]

Are we not already analyzing exactly the same problem in https://www.physicsforums.com/threads/two-bodies-hanging-from-pulley.1011640/

The two masses there have a different ratio, but it is otherwise the identical situation.

Yes, the situations are identical, although the questions asked are slightly different. Here the problem asks for the downward force on the pulley (I assume) while the other thread asks for acceleration.

But you're right, it's essentially the same problem.

I'll leave this open for a bit, in case it was the wording of the problem that was throwing him. (Thanks for flagging this.)

 

[kuruman]

But I think this is wrong eqn.

Why do you think it is the wrong equation? It was the correct equation in the other Atwood machine problem. As @Doc Al suggested, you need to find the tension in the rope. The equation you quoted here will not give it to you because the tension drops out as it is supposed to do.

In the other problem, you had a system of 2 equations and 2 unknowns, the tension and the acceleration. By eliminating the tension you got an equation involving the acceleration only. That's the equation you quoted here. Go back to the system of 2 equations in the previous problem and eliminate the acceleration to get an equation involving only the tension.

 

[haruspex]

$(T-m1g)-(T-m2g)=(m1+m2)a$
But I think this is wrong eqn.

It is a correct equation, though perhaps not the best approach to the problem. In what sense do you think it is wrong? That it won't help answer the question or that it will produce the wrong answer? Those will depend on how you use the equation. What was your next step?

 

[rudransh verma]

Why do you think it is the wrong equation? It was the correct equation in the other Atwood machine problem. As @Doc Al suggested, you need to find the tension in the rope. The equation you quoted here will not give it to you because the tension drops out as it is supposed to do.

In the other problem, you had a system of 2 equations and 2 unknowns, the tension and the acceleration. By eliminating the tension you got an equation involving the acceleration only. That's the equation you quoted here. Go back to the system of 2 equations in the previous problem and eliminate the acceleration to get an equation involving only the tension.

O yes!

 

[rudransh verma]

In the other problem, you had a system of 2 equations and 2 unknowns, the tension and the acceleration. By eliminating the tension you got an equation involving the acceleration only. That's the equation you quoted here. Go back to the system of 2 equations in the previous problem and eliminate the acceleration to get an equation involving only the tension.

On taking g= 10 I got 2T= 53.34 N
On taking g= 9.8 I got 2T=52 N
Official answer is 54 N.

 

[jbriggs444]

On taking g= 10 I got 2T= 53.34 N
On taking g= 9.8 I got 2T=52 N
Official answer is 54 N.

Always show your work. However, your results fit with what I get, while the official answer does not.

The approach I took was to note that all the masses share the same speed. We have a net unbalanced gravitational force of 2mg. We have a total inertia of 6mg. So it is immediately clear that the acceleration of the masses will be $\frac{1}{3}g$.

If the left hand (heavy) mass is accelerating down at $\frac{1}{3}g$ then tension must be supporting $\frac{2}{3}$ of its weight. That's $\frac{8}{3}g$ Newtons

If the right hand (light) mass is accelerating upward at $\frac{1}{3}g$ then tension must be providing $\frac{4}{3}$ of its weight. That's $\frac{8}{3}g$ Newtons

Sanity check: The two tensions match, as they must.

Total of the two tensions is $\frac{16}{3}g$ Newtons

To a reasonably appropriate number of significant digits...
With $g=9.80665$ I get $52.3021$ Newtons
With $g=9.8$ I get $52$ Newtons
With $g=10.$ I get $53$ Newtons.

I see no way to justify rounding $53.\overline{3}$ up to $54$ unless one has a deathly fear of odd numbers or a monstrously huge slab of depleted Uranium under the lab.

 

[rudransh verma]

I see no way to justify rounding 53.3― up to 54 unless one has a deathly fear of odd numbers or a monstrously huge slab of depleted Uranium under the lab.

I want to ask does using one pulley minimises the effort needed to pull a mass up. I don’t think this is true. $F=m_1g+m_1a$ and if we use a pulley then $F-T+T-m_1g=m_1a$

 

[Steve4Physics]

I want to ask why does we need more effort to pull a mass up directly as compared to using a pulley.
As I know Tension T required to pull up will be $T=m_1g+m_1a$. But when we use a pulley the force will be $(m_1+m_2)a+m_1g$ to create the same acceleration a. So how is this force more than T?

Avoid introducing terms like ‘effort’ unless you define them. By ‘effort’, do you mean the net force on an object? Or the tension? Or something else?

Your first equation is OK: $T=m_1g+m_1a$.

But the second equation isn't clear:
force = $(m_1+m_2)a+m_1g$
You haven’t said which ‘force’ you mean.
And this equation ignores $m_2$’s weight - there is no term $m_2g$.

Maybe you can clarify the question.

 

[rudransh verma]

But the second equation isn't clear:

I was wrong with second eqn. I edited it. The force F required to pull mass m1 will be same $m_1g+m_1a$ whether we use a pulley or not. To take the advantage of pulley we need to add an extra weight. I hope I am right!

 

[Steve4Physics]

I was wrong with second eqn. I edited it. The force F required to pull mass m1 will be same $m_1g+m_1a$ whether we use a pulley or not.

The net force on $m_1$ is $F_{net,1} = m_1a$. The tension in the rope is $T =m_1g+m_1a$.
Take care to be absolutely clear to which of these you are referring, or it introduces confusion.

To take the advantage of pulley we need to add an extra weight. I hope I am right!

It depends what you mean by 'advantage'.

The main advantage of a single pulley in practical use is that it changes the direction of the required force. It is often easier to raise a weight by pulling downwards rather than by applying an upwards force.

With an Atwood machine arrangement, you are raising a weight by allowing another weight (counterweight) to descend. This is rather like using a counterwight in a simple elevator:
https://www.researchgate.net/profile/Bolarinwa-Gabriel-Oladeji-2/publication/281288070/figure/fig2/AS:284481790464018@1444837152552/Arrangement-of-hoisting-rope-cabin-and-counterweight_Q320.jpg

 

[rudransh verma]

The net force on m1 is Fnet,1=m1a. The tension in the rope is T=m1g+m1a.
Take care to be absolutely clear to which of these you are referring, or it introduces confusion.

I am referring to T which is created by weight and acceleration. This will be the force necessary to lift m1.

It depends what you mean by 'advantage'.

I meant to reduce the necessary force to lift we need pulley and counter weight.