- #1
zorro
- 1,384
- 0
Homework Statement
The Attempt at a Solution
Is there any difference between the above expression and
Is there any relation between these two?
Exploring the Binomial Series: A Comprehensive Homework Statement
In summary, the conversation discussed the difference and relation between two expressions involving sigma signs and C values. The first expression has one sigma sign and a specific requirement for the values of r and s, while the second expression has two sigma signs and no specific requirement. It was also mentioned that the second expression has roughly double the terms of the first, and an exact equation for the difference between the two was requested. After some calculations, the answer was successfully found.
Is there any difference between the above expression and
Is there any relation between these two?
- #2
VietDao29
Homework Helper
- 1,426
- 3
Abdul Quadeer said:Homework Statement
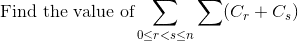
Are you sure there are up to 2 sigma signs in that expression? By the way, you mean [tex]C_r^n[/tex] right?
If there's just one sigma, then [tex]\sum_{0 \le r < s \le n} (C_r^n + C_s^n)[/tex] is different from [tex]\sum_{r = 0}^n \sum_{s = 0}^n (C_r^n + C_s^n)[/tex].
In the first sum [tex]\sum_{0 \le r < s \le n} (C_r^n + C_s^n)[/tex], r, and s can take any value raging from 0 to n, but r must be less than s.
However, in the second sum: [tex]\sum_{r = 0}^n \sum_{s = 0}^n (C_r^n + C_s^n)[/tex], r, and s can take any value raging from 0 to n, no more requirement is needed.
So, in general, the second sum will have more terms than the first sum.
- #3
tiny-tim
Science Advisor
Homework Helper
- 25,839
- 258
Hi Abdul! 
The second one is roughly double the first, since it contains eg C1 + C2 but not C2 + C1.
The second one is roughly double the first, since it contains eg C1 + C2 but not C2 + C1.
hmm … what about all the terms such as C1 + C1 ?
can you find an exact equation for the difference between the second and twice the first?
can you find an exact equation for the difference between the second and twice the first?
- #4
zorro
- 1,384
- 0
VietDao29 said:
Yeah there are 2 sigma signs. 0<=r<s<=n is in between the two sigma signs.
tiny-tim said:
Does that equate to
- #5
tiny-tim
Science Advisor
Homework Helper
- 25,839
- 258
Yes, except i'd call it 2 ∑Cr
ok now write ∑∑ (Cr + Cs) over all r and s in terms of ∑Cr
(try it first with an easy small number for n, like n = 3, if you're stuck)
ok now write ∑∑ (Cr + Cs) over all r and s in terms of ∑Cr
(try it first with an easy small number for n, like n = 3, if you're stuck)
- #6
zorro
- 1,384
- 0
Thanks!... I got the answer
FAQ: Exploring the Binomial Series: A Comprehensive Homework Statement
What is the Binomial Series?
The Binomial Series is a mathematical concept that represents the expansion of a binomial expression, such as (a+b)^n, into a series of terms. It is used to solve problems in algebra, calculus, and statistics.
How is the Binomial Series used in mathematics?
The Binomial Series is used to approximate functions and solve problems involving binomial expressions. It can also be used to find the coefficients of a polynomial and to expand the power of a binomial to any positive integral power.
What is the formula for the Binomial Series?
The formula for the Binomial Series is (a+b)^n = a^n + nC1 * a^(n-1) * b + nC2 * a^(n-2) * b^2 + ... + nCr * a^(n-r) * b^r + ... + nCn * b^n, where n is a positive integer and nCr is the combination formula.
What are some real-life applications of the Binomial Series?
The Binomial Series has many real-life applications, including in finance, physics, and engineering. It is used to calculate probabilities in statistics, model physical systems in physics, and approximate complex functions in engineering.
What is the importance of understanding the Binomial Series?
Understanding the Binomial Series is important because it is a fundamental concept in mathematics and has many practical applications. It also helps to develop problem-solving skills and critical thinking in various fields of study.