- #1
Rev. Cheeseman
- 333
- 20
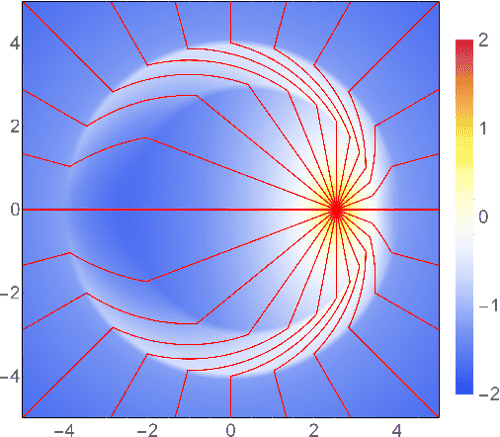
How does an electric field of a moving charge, for example a moving electron, inside a wire looks like? Does it looks like this with distorted circular radial lines?