Exploring the Electric Field of a Moving Charged Spherical Shell

[Povel]

TL;DR Summary

Assuming that a charged spherical shell is moving inertially, would an accelerated observer (test charge) inside of it detect an electric field?

The electric field inside a charged spherical shell moving inertially is, per Gauss's law, zero.

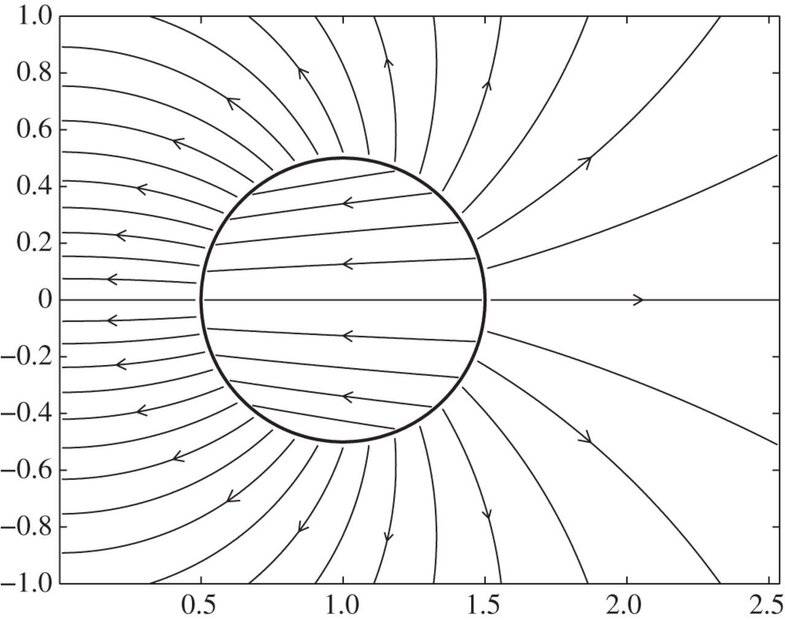
If the spherical shell is accelerated, the field inside is not zero anymore, but it gains a non-null component along the direction of the acceleration, as mentioned, for example, in this paper.

The following picture from the above paper shows the field lines in the xy-plane in the instantaneous rest frame. The shell is undergoing rigid hyperbolic motion along the x-axis (toward the right)

The question I have is the following:

Assuming that a charged spherical shell is moving inertially, would an accelerated observer (test charge) inside of it detect an electric field like in the image above?

This question is also equivalent to asking the following ones:

Is there an electric field inside the shell if it is accelerating in an homogenous gravitational field? Will an observer (test charge) in the center of the shell that is not falling along with it, detect an electric field?

I read in a couple of papers that there won't be any field detected by such observer, but this is not demonstrated and sounds strange to me.
The reasoning of these papers is that the electromagnetic tensor is invariant, so if it is zero in the inertial frame it will be zero also in the non-inertial one.

But here we are talking about the electric field only, which is a component of the electromagnetic tensor, so I don't see any a priori reason why it could not be made non-zero thanks to a frame transformation.

My reasoning for being dubious about this is that, intuitively, if one zooms out from the shell and looks at it from the distance, it will look like a point particle, and its field will also look like that of a point particle. As it has been detailed in numerous papers throughout the years (spanning over half a century), an accelerated observer looking at a point charge that moves inertially will detect continuous radiation coming from it. (An accelerated observer at rest relative to a co-accelerated point charge sees instead only a static Coulomb field).

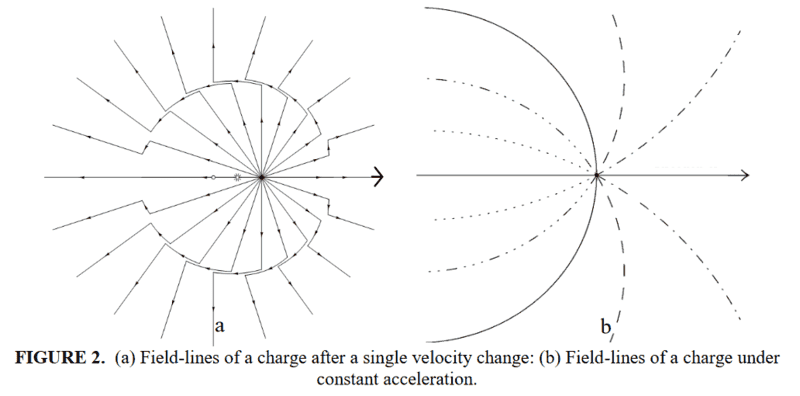This then seems to imply to me that, if we consider that point charge to be the charged shell as seen from the distance, then for such distant observer the exterior electric field will look just like in the first picture, and therefore I would also expect the interior field, when seen close up, to look the same.

 

[Andrew Mason]

I don't see how these facts could exist. How could the test charge not be affected by an electric field from some source? If the test charge is accelerating relative to the shell, the force causing that acceleration has to be electrical. It can't be gravity and there isn't anything else.

AM

 

[Vanadium 50]

This question is also equivalent to

No, it's not.

TL;DR Summary: Assuming that a charged spherical shell is moving inertially, would an accelerated observer (test charge) inside of it detect an electric field?

I read in a couple of papers

That's not so helpful if we don't know which ones.

It seems to me that you have three or more questions in there, all tangled up with various assumptions. I think it's very unlikely that this will clear anything up for you - continued confusion is likely the best possible outcome.

I suggest you try again without asking a compound question.

 

[anuttarasammyak]

TL;DR Summary: Assuming that a charged spherical shell is moving inertially, would an accelerated observer (test charge) inside of it detect an electric field?

Assuming that a charged spherical shell is moving inertially, would an accelerated observer (test charge) inside of it detect an electric field like in the image above?

Yes, I think so. The Fermat metric of Rindler coordinate, ref. https://en.wikipedia.org/wiki/Rindler_coordinates, should make an inhomogeneous point charge distribution on the "rigid" spherical shell "in inertial motion" as in the picture you attached though "rigid" and "in inertial motion" might have to be well considered.

TL;DR Summary: Assuming that a charged spherical shell is moving inertially, would an accelerated observer (test charge) inside of it detect an electric field?

I read in a couple of papers that there won't be any field etected by such observer, but this is not demonstrated and sounds strange to me.

I also feel uneasy on such a conclusion. Can I read some of them on website ?

I think even in SR, say the charged spherical shell is at rest in a IFR, an observer in another IFR observes not zero electric field inside the shell as
$$E^2-H^2=0$$
in Gaussian unit where H is magnetic field generated by motion of charges on the shell.

 

[Vanadium 50]

Rindler

I don't think it needs to get that complicated. It's hard to tell, since untangling the question from the assumptions needs to be done, and the OP has come back but declines to clarify. However, charges on the shell are in relative motion (as is the shell shape), so some observers see magnetic forces. That means other observers see electric forces.

 

[Povel]

Sorry for the silence, this week I didn't have and still don't have any moment to reply properly. I should be able to do so and clarify my question better over the next days, hopefully. Thanks in advance for all your replies

 

[Povel]

I don't see how these facts could exist. How could the test charge not be affected by an electric field from some source? If the test charge is accelerating relative to the shell, the force causing that acceleration has to be electrical. It can't be gravity and there isn't anything else.

AM

I did not stipulate any special property to the test charge mentioned in the question, so in an actual setup it might be represented by any sort of charged macroscopic object / electric field detector, as long as its presence doesn't alter the system in a significant way. Its acceleration could be caused then by any type of force. For example, it could be mounted on tiny rocket, or launched by a spring mechanism.

Of course, if the test charge in question is an actual charge particle, then as you point out it will require the action of some electromagnetic field to accelerate.
I think that in this situation it would still make sense to ask if, on top of the accelerating electric field, the particle is under the influence of an electric field from the surrounding charged shell.

I suppose that one could also completely ignore any test charge and simply ask what electric field, if any, appears in an accelerated frame inside the shell due to the shell charge distribution and relative motion.

 

[Povel]

No, it's not.

That's not so helpful if we don't know which ones.

It seems to me that you have three or more questions in there, all tangled up with various assumptions. I think it's very unlikely that this will clear anything up for you - continued confusion is likely the best possible outcome.

I suggest you try again without asking a compound question.

Sorry I didn't post it here to not overload my initial post. Here is one of the papers in question The relevant passage is at page 1720 (26 in the pdf). Quoting from it:

Consider an inertial, i.e., freely falling, uniformly charged spherical shell. The shell is sufficiently small that tidal effects may be neglected.
With reference to the inertial rest frame of the shell, it is a consequence of elementary electromagnetic theory that the electromagnetic field vanishes inside the shell. Neither is there an electromagnetic field relative to an
accelerated frame inside the shell, due to the invariance of a vanishing electromagnetic field.

It may be argued that if only relative motion matters, the electromagnetic field determined by an inertial observer inside an accelerated charged shell should be the same as that determined by an accelerated observer inside an inertial shell. Since the latter field vanishes, it is tempting to conclude that an inertial observer inside an accelerated charged shell should not observe any electromagnetic field.
However, a calculation based upon electromagnetic theory shows that an inertial observer in an accelerated charged shell should observe a nonvanishing electromagnetic field. [..]

According to the above results of the Einstein-Maxwell theory the two situations, (I) accelerated observer-inertial shell and (II) inertial observer-accelerated shell, are not equivalent. The electromagnetic field inside a
uniformly charged sphere vanishes if and only if the shell is inertial.
Let us consider in some detail the case of an inertial shell as described by an accelerated observer. According to the Maxwell-Einstein theory he observes the electrical field from a freely falling point charge to be a Lorentz contracted Coulomb field attached to the charge. Integration over the surface of the shell leads to the result that the accelerated observer will not observe any electrical field inside the shell.
In situation (II) both the inertial observer and an accelerated observer comoving with the shell will observe a nonvanishing electrical field. The comoving observer finds himself to be at rest inside a static shell in the
presence of a uniform gravitational field. According to the covariant form of electromagnetic theory as applied to Rindler space, the electrical fieldlines from a stationary point charge are shaped like the water rays in a spherical fountain. Integration over the spherical shell now gives a nonvanishing electrical field in the downward direction inside the shell.

Concerning my assumptions, I'm not sure how to disentagle them up, but I hope that by reading the above quoted passage and/or the paper you can see where the other additional question(s) came from.

 

[Povel]

Yes, I think so. The Fermat metric of Rindler coordinate, ref. https://en.wikipedia.org/wiki/Rindler_coordinates, should make an inhomogeneous point charge distribution on the "rigid" spherical shell "in inertial motion" as in the picture you attached though "rigid" and "in inertial motion" might have to be well considered.

I also thought about Rindler coordinates, though I'm not capable to calculate what the charge distribution on the inertial shell would look like.

I also feel uneasy on such a conclusion. Can I read some of them on website ?

I think even in SR, say the charged spherical shell is at rest in a IFR, an observer in another IFR observes not zero electric field inside the shell as
$$E^2-H^2=0$$
in Gaussian unit where H is magnetic field generated by motion of charges on the shell.

I posted the paper reference and the passage in my previous post.

Could you please elaborate on this? Why this invariant being zero means that there is a non-zero electric field inside the shell?

Intuitively, I also think that a shell moving with a certain velocity relative to an IFR should produce a magnetic field inside of it.

If I imagine to section the shell along its parallels (with the axis having the same direction of the shell velocity), I obtain rings of different sizes moving all perpendicularly to their diameter.
Using the right-and rule, then, It would seem that each ring would generate an internal magnetic field with opposite direction compared to the external one. Summing them all up, there should be a non-null magnetic field inside the shell.

 

[anuttarasammyak]

I don't think it needs to get that complicated. It's hard to tell, since untangling the question from the assumptions needs to be done, and the OP has come back but declines to clarify. However, charges on the shell are in relative motion (as is the shell shape), so some observers see magnetic forces. That means other observers see electric forces.

I also thought about Rindler coordinates, though I'm not capable to calculate what the charge distribution on the inertial shell would look like.

I agree with you feeling annoyance in dealing with accerelation. As I wrote in the end of my post and Povel shows curiousity to it,

Could you please elaborate on this? Why this invariant being zero means that there is a non-zero electric field inside the shell?

, I recommed him to investigate this SR case,i,e, transformation of electromagnetic fields between two IFRs, at leat at first. It will be interesting enough.　

13–6The relativity of magnetic and electric fields​

https://www.feynmanlectures.caltech.edu/II_13.html is a good piece to learn.

 

[Ibix]

Is the question just "what field is seen inside an inertially moving charged spherical shell by an accelerating observer?" If so, surely the answer is trivial. In the rest frame of the shell the electric field and the magnetic field are zero, thus the EM tensor is zero. Thus it is zero in all coordinate systems because the coordinate transforms are just matrix multiplications. Or am I misunderstanding the question?

 

[anuttarasammyak]

Is the question just "what field is seen inside an inertially moving charged spherical shell by an accelerating observer?" If so, surely the answer is trivial. In the rest frame of the shell the electric field and the magnetic field are zero, thus the EM tensor is zero. Thus it is zero in all coordinate systems because the coordinate transforms are just matrix multiplications. Or am I misunderstanding the question?

Thanks for good insights. Let me confirm in basic SR case.

Say a charged spherical is at rest in an IFR. Inside the shell : E =0, B=0.
In another IFR for the same time-space points : E'=0, B'=0.

Is it right?

 

[Ibix]

Is it right?

All coordinate systems, not just inertial frames, and it's not limited to special relativity. If all components of a tensor are zero in one coordinate system they must be zero in any coordinate system.

 

[anuttarasammyak]

@Ibix Thanks for confirmation. I feel amazing that :
- moving spherical charges do not generate magnetic field inside.
- moving thus Lorentz contracted charged sphere do not generate electric field inside.

 

[Ibix]

I feel amazing that :
- moving spherical charges do not generate magnetic field inside.
- moving thus Lorentz contracted charged sphere do not generate electric field inside.

Remember that the fields from isolated moving charges are not spherically symmetric.

So we may say Unruh effect in acceleration system have nothing to do with electromagnetic field, e.g. photon generation or absorption does not happen by Unruh effect.

This is purely classical. The Unruh effect is from quantum field theory and I don't know enough about it to comment.