Exploring Variation in Slopes of Horizontal Asymptotes in Rational Functions

[scott_alexsk]

Hello,

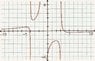
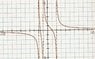
Recently I have been trying to reason why certain rational functions such as (-2(2x^2+x-31))/((x-3)*(x+4)*(x+1)) have varying near horizontal asymptote slopes. I know that the direction of the horizontal asymptote can be varied by altering the parent function x+1/x, but several equations like the one above do not duplicate the single line or single slope that variations of that parent equation produce.

So I quess my question is, in rational functions what causes variation in the slope of horizontal asymptotes?

I have been able to glean that when the number of roots on top of the rational function is greater than or equal to the number on the bottom, the slope of the asymptotes is something besides 0. Also it seems that the slopes of the horizontal asymptotes vary from each other when there are 1 or more complex roots in the dividend of the equation.

Thanks,
-scott

 

[HallsofIvy]

?? horizontal asymptotes always have slope 0!

I assume you really mean non-horizontal, slanting, asymptotes.

The original function you post, (-2(2x^2+x-31))/((x-3)*(x+4)*(x+1)), since it has degree in the denominator higher than the degree in the numerator has y= 0 as asymptote which is horizontal.
But I don't know what you mean by "parent function". Certainly, x+ 1/x has y= x as asymptote because, as x goes to either plus or minus infinity, the 1/x part goes to 0. In what sense is that a "variation" of (-2(2x^2+x-31))/((x-3)*(x+4)*(x+1)) ?

If the degree of the numerator is less than the degree of the denominator, then y= 0 is a horizontal asymptote.

If the degree of the numerator equals the degree of the denominator, then y= a is a horizontal asymptote where a is the ratio of the leading coefficients.

If the degree of the numerator is one more than the degree of the denominator then there is a slant asymptote with slope equal to the ratio of the leading coefficients.

If the degree of the numerator is two or more larger than the degree of the denominator, the asymptote is a curve (although many people would not use the word "asymptote" in that case, reserving it for lines).

 

[scott_alexsk]

Well in the case of that equation the near-horizontal asymptotes have a slope that looks like 1/infinity and 0.5/infinity. Most importantly the lines seem to follow two different asymptotes. How would you find the slope of these two lines from the equation?

Thanks,
-scott

 

[arildno]

(any number)/(members of a number sequence tending towards infinty) tends to zero.

 

[HallsofIvy]

Well in the case of that equation the near-horizontal asymptotes have a slope that looks like 1/infinity and 0.5/infinity. Most importantly the lines seem to follow two different asymptotes. How would you find the slope of these two lines from the equation?

Thanks,
-scott

It's not clear to me what line you are talking about. The first example you gave, for large x, is close to -4/x which goes to 0. The second you wrote as x+ 1/x which has y= x (with slope 1). Did you mean (x+ 1)/x? That is equivalent to 1+ 1/x which has y= 1 as a horizontal asymptotes.

In any case, "1/infinity" and "0.5/infinity" are both 0. There are no two different lines.
These are not "near-horizontal", the asymptotes are horizontal.

 

[scott_alexsk]

Sorry about my incorrect description, I did not have that much time this morning.

Anyways attached are two diagrams. The first is the graph of the equation I have been mentioning and the second is an example of a less 'messy' rational function, ((3x+5)*(x-1))/((x+1)*(x-2)*(x+1)).

What bugged me about the first equation, (-2(2x^2+x-31))/((x-3)*(x+4)*(x+1)), is that, as opposed to the second graph, the the lines converging on the asymptote X=0 bend inward instead outward to that asymptote. By the way I meant x+(1/x). Thank you guys very much for your time. I truly appreciate it.

-scott

 

[Robokapp]

$${-2(2x^2+x-31)}/{(x-3)(x+4)(x+1)}$$

It's bottom heavy...unless you mised an x somewhere.

 

[HallsofIvy]

$${-2(2x^2+x-31)}/{(x-3)(x+4)(x+1)}$$

It's bottom heavy...unless you mised an x somewhere.

Yes, that's his point. It and the other function he mentions both have horizontal asymptote y= 0. Although in his first post scott_alexsk said "I know that direction of the horizontal asymptote can be varied", I think he is really talking about how the curve approaches the horizontal asymptote.

If that is the case, then it depends on the leading coefficients.
The leading coefficient of the numerator of ((3x+5)*(x-1))/((x+1)*(x-2)*(x+1)) clearly will be 3 while the leading coefficient in the denominator will be 1. For very large the function value will be close to 3/x and will approach the asymptote y= 0 like 3/x does.

The leading coefficient of the numerator of (-2(2x^2+x-31))/((x-3)*(x+4)*(x+1)) is -4 while the leading coefficient of the denominator is 1. For very large x, the function value will be close to -4/x. I'm not sure what "bend inward instead outward" means but I suspect it is due to that negative coefficient.

 

[scott_alexsk]

Well just to clarify, I am referring to the interesting feature in the first graph. It looks as if the line to the far left has been translated up 1 unit, but it still bends towards Y=0. The same is with the line on the far right in the first graph, instead translated down about 0.5 units.

Personally I do not think that the negative 2 does this. After playing around with the equation 1/(x-1)^2, it seems to me that this feature stems from the incomplete square in the dividend of the equation. When I factor out the equation I get 1/(x^2-2x+1). By simply removing the 1 I get a dramtically changed slope from the orginally horizontal asymptote. But this is just a thought.

Thank you for your time,
-scott

 

[uart]

Scott, I was also initially unsure about exactly what you were asking but I think the "thing that bugs you" about the first equation is nothing more than that fact that a zero occurs between the last pole and the asymptote.

Just solve for the zeros in the numerator and you'll see that's all it is, after the last pole the curve has to come back down through zero before finally going back to zero along the asymptote.

 

[scott_alexsk]

No it is not that but the fact that the line moves to the other side then bends back towards y=0 unlike most rational function lines, which stay on one side and bend (outwardly) towards the asymptote. I want to see the reason why it does this, unlike most other rational functions.

-scott

 

[uart]

No it is not that but the fact that the line moves to the other side

Moves to the "other side". What the hell is that if it's not a zero crossing. Like I said before, this happens because there is a zero in the numerator between the last pole (zero of the denominator) and the asymptote.

 

[scott_alexsk]

OK that was part of it, but what I am most concerned about is what causes the line to apparently be translated up but to bend back to the y=0 asymptote, unlike most other rational functions I have seen (like the one in the tumbnail to the right in one of my prior posts).

-scott

 

[Office_Shredder]

I think he's talking about how the graph in the first thumbnail crosses the asymptote line

 

[scott_alexsk]

HOI, you were right, it is the negative 2 that does it, in combination with the -31 and the 2x^2. In the initial positive x-values, y remains positive because of the -31*-2, but eventually the 2x^2+x catches up and bends it the other direction. Sorry for the delay in understanding. Thanks to everyone to posted in this thread.

-scott