- #1
Joshuaniktas
- 1
- 0
Hi there, I have tried to do these questions but I don't understand. Any help would be appreciated!
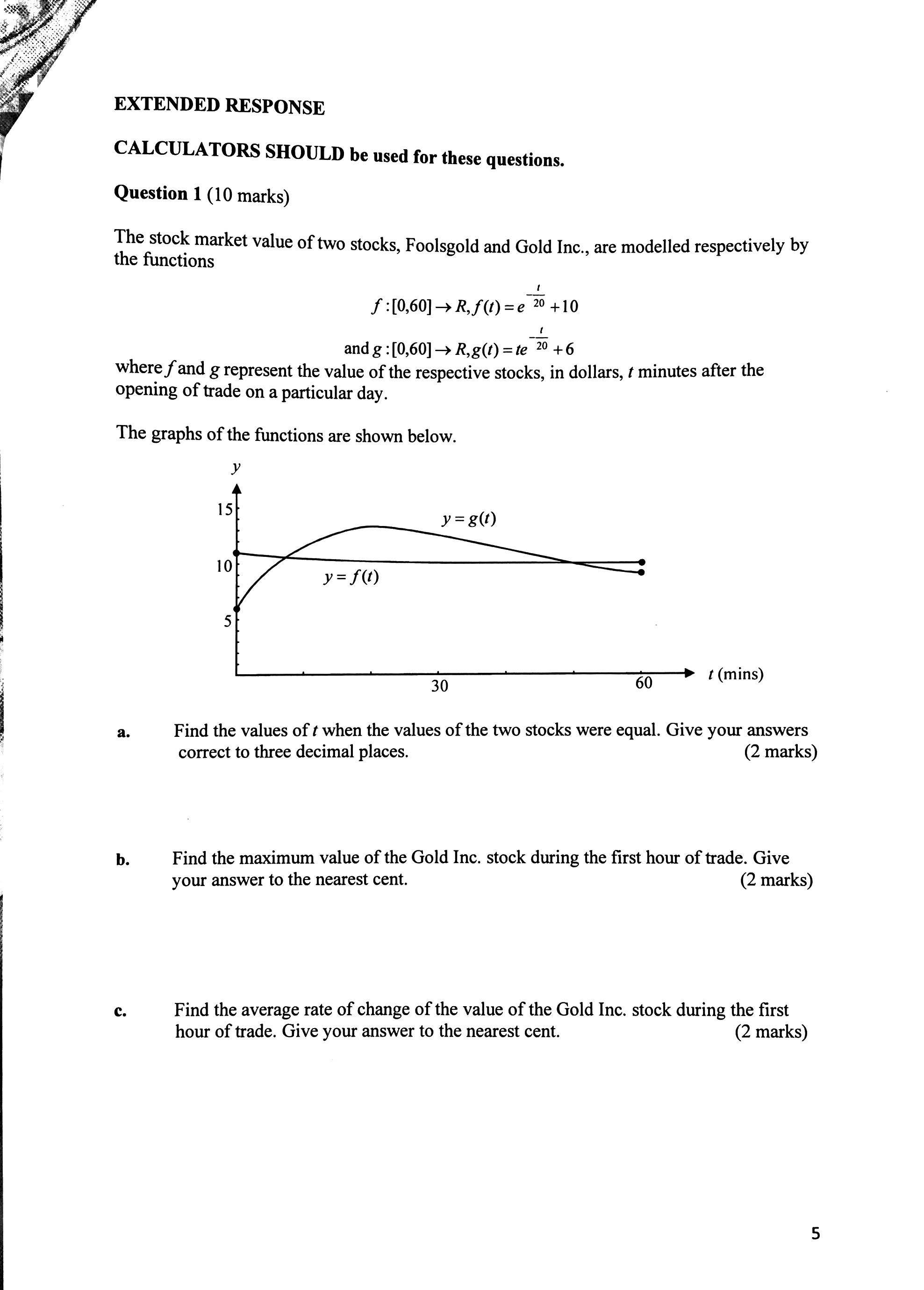
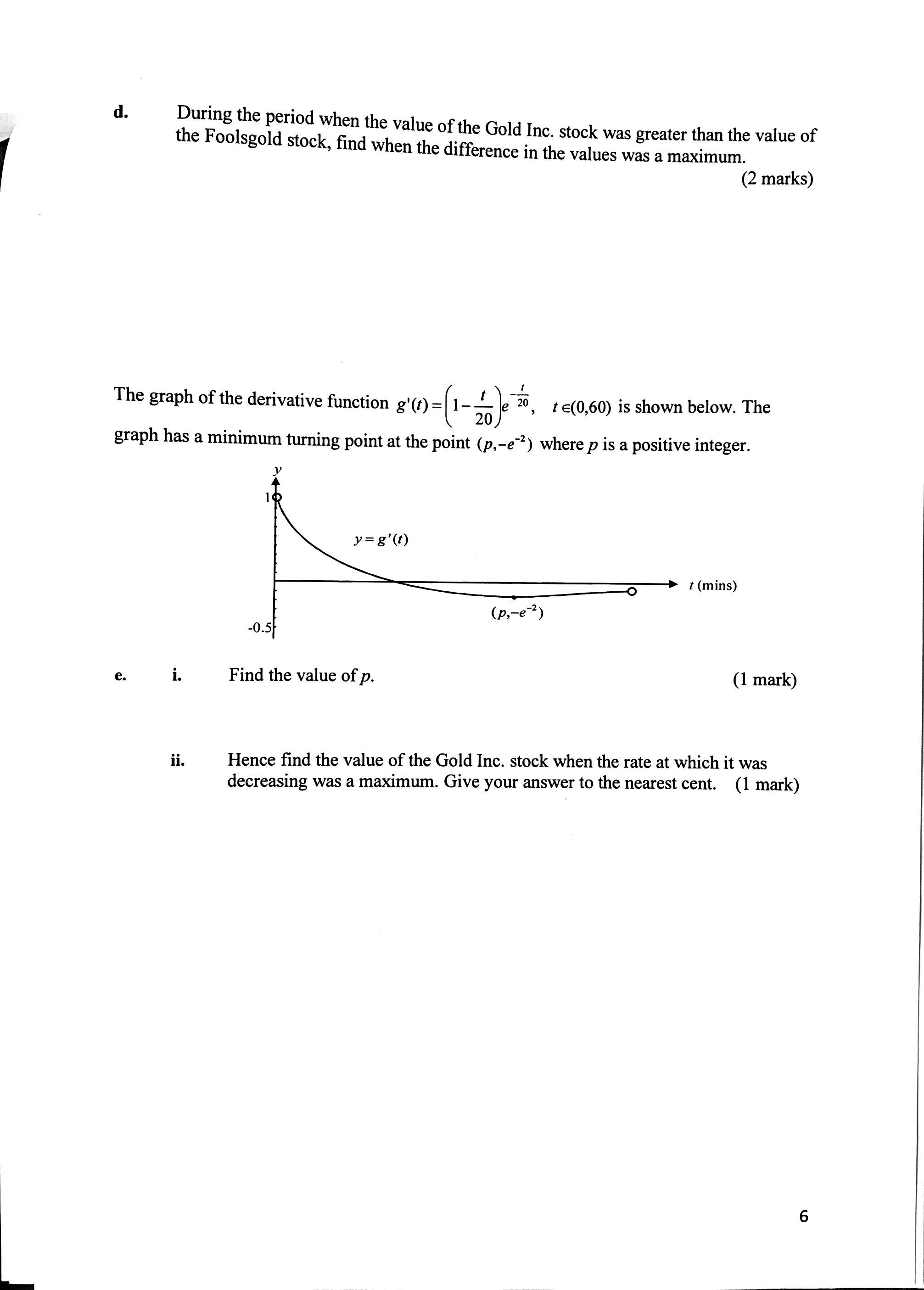
An exponential function is a mathematical function of the form f(x) = ab^x, where a and b are constants and x is the independent variable. This type of function is characterized by a constant ratio between the output and the input, resulting in a curve that increases or decreases rapidly.
To graph an exponential function on a calculator, you first need to enter the function into the calculator using the appropriate syntax. Then, you can use the graphing function of the calculator to plot the points and draw the curve. Some calculators also have a built-in table function that can display a table of values for the function.
The main difference between an exponential function and a linear function is that the rate of change, or slope, in an exponential function is not constant. In a linear function, the rate of change is constant, resulting in a straight line. Additionally, exponential functions have a constant ratio between the output and the input, while linear functions have a constant difference between the output and the input.
To solve exponential functions using a calculator, you can use the exponential function button (usually denoted as "exp" or "e^x") to input the function into the calculator. Then, you can use the calculator's solve function to find the value of the independent variable that satisfies the equation. Some calculators also have a logarithm function that can be used to solve exponential functions.
Exponential functions are commonly used in fields such as finance, biology, and physics. Some real-life applications include population growth, compound interest, radioactive decay, and bacterial growth. They can also be used to model the spread of diseases, the growth of technology, and the decay of natural resources.