Exponential potential energy state diagram

[ThEmptyTree]

Homework Statement

A particle of mass $m$ moves in one dimension. Its potential energy is given by $$U(x) = −U_0e^{-x^2/a^2}$$ where $U_0$ and $a$ are constants.
(a) Draw an energy diagram showing the potential energy $U(x)$. Choose some value for the total mechanical energy $E$ such that $−U_0 < E < 0$. Mark the kinetic energy, the potential energy and the total energy for the particle at some point of your choosing.
(b) Find the force on the particle as a function of position $x$. Express you answer in terms of some or all of the following: $x, a,$ and $U_0$.
(c) Find the speed at the origin $x = 0$ such that when the particle reaches $x = \pm a$, it stops momentarily and reverses the direction of its motion. Express you answer in terms of some or all of the following: $x, a, m$ and $U_0$.

Relevant Equations

For one-dimensional kinematics $$F_c=\frac{dU}{dx}$$

It is my second "energy state diagram problem" and I would want to know if I am thinking correctly.

First I have done some function analysis to get a glimpse of the plot:
- no roots but $\lim\limits_{x\to-\infty}U(x)=\lim\limits_{x\to+\infty}U(x)=0$
- y interception: $U(0)=-U_0$
- even function: $U(x)=U(-x)$
- first derivative: $\frac{dU(x)}{dx}=\frac{2U_0x}{a^2}e^{-x^2/a^2}$ so the function is decreasing on $(-\infty;0)$ but increasing on $(0;+\infty)$

So my answer at (a):

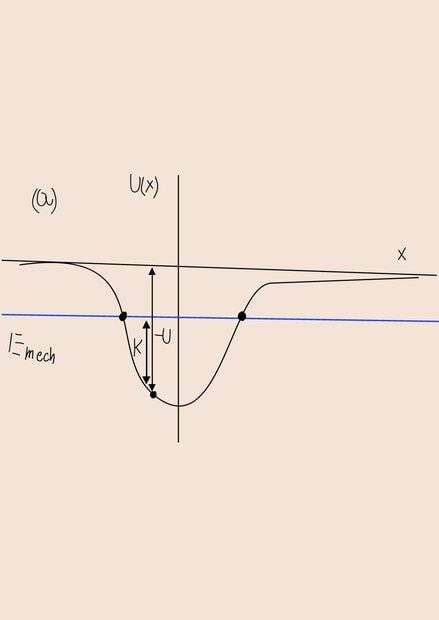(b) Using the fact that the net conservative force is the space derivative of potential: $$F_c(x)=\frac{2U_0x}{a^2}e^{-x^2/a^2}$$

(c) Turnaround points are at $x=\pm a$ which is solution to the equation $U(x)=E_{mech}$
So $E_{mech}=-\frac{U_0}{e}$
At the origin $E_{mech}=K(0)+U(0)=\frac{1}{2}mv_0^2-U_0\Rightarrow v_0=\sqrt{2\Big(1-\frac{1}{e}\Big)\frac{U_0}{m}}$

Is it ok?

 

[haruspex]

All looks good.

 

[ThEmptyTree]

All looks good.

Thanks!

Just a quick off-topic question pleaase
In my physics book it states that "Power is the ratio between work $W$ done by a force during a time interval $\Delta{t}$ and the time interval. Hence $P_{ave}=\frac{W}{\Delta{t}}=\vec{F}\cdot\vec{v_{ave}}$."

My attempt to prove: $\vec{F}\cdot\vec{v_{ave}}=\vec{F}\cdot\frac{\Delta{\vec{r}}}{\Delta{t}}$. The next step would be to say that $\vec{F}\cdot\Delta{\vec{r}}=W$ but isn't this true only for one-dimensional motion? From what I've learned for non uniform path the work is the line integral of the scalar product between the force and the infinitesimal displacement. Then for non uniform path the average power is $P_{ave}=\frac{W_{ave}}{\Delta{t}}$ ?

 

[Orodruin]

If F = dU/dx, then F points towards regions with higher potential. Think about if this makes sense or not.

 

[ThEmptyTree]

If F = dU/dx, then F points towards regions with higher potential. Think about if this makes sense or not.

When the potential is increasing (positive derivative) the force is negative (points to the left) and when the potential is decereasing (negative derivative) the force is positive (points to the right). Related to that, one analogy that we can make is that the graph metaphorically represents the motion of a ball that slides down the hill starting from a point below the mechanical energy, but doesn't have enough kinetic energy to get past the turnaround point, so it's "trapped" in the hill. I understand that.

Thanks!

Just a quick off-topic question pleaase
In my physics book it states that "Power is the ratio between work $W$ done by a force during a time interval $\Delta{t}$ and the time interval. Hence $P_{ave}=\frac{W}{\Delta{t}}=\vec{F}\cdot\vec{v_{ave}}$."

My attempt to prove: $\vec{F}\cdot\vec{v_{ave}}=\vec{F}\cdot\frac{\Delta{\vec{r}}}{\Delta{t}}$. The next step would be to say that $\vec{F}\cdot\Delta{\vec{r}}=W$ but isn't this true only for one-dimensional motion? From what I've learned for non uniform path the work is the line integral of the scalar product between the force and the infinitesimal displacement. Then for non uniform path the average power is $P_{ave}=\frac{W_{ave}}{\Delta{t}}$ ?

^ That was a separate question for a completely different thing.

 

[haruspex]

The next step would be to say that $\vec{F}\cdot\Delta{\vec{r}}=W$ but isn't this true only for one-dimensional motion? From what I've learned for non uniform path the work is the line integral of the scalar product between the force and the infinitesimal displacement.

I don't see any contradiction. If $\vec{F}\cdot\Delta{\vec{r}}=\Delta W$ (your version omitted the delta) then $W=\int \vec{F}\cdot d{\vec{r}}$.

 

[ThEmptyTree]

I don't see any contradiction. If $\vec{F}\cdot\Delta{\vec{r}}=\Delta W$ (your version omitted the delta) then $W=\int \vec{F}\cdot d{\vec{r}}$.

I did not omit the delta. This is what says in my book. However I agree with the delta.

As of what I know, we can only integrate if we are working with infinitesimal quantities, whereas $\Delta{\vec{r}}$ and $\Delta{t}$ are finite quantities as described in my book.

 

[haruspex]

I did not omit the delta.

I wrote that your version omitted the delta, not that you were responsible for the omission.

As of what I know, we can only integrate if we are working with infinitesimal quantities, whereas $\Delta{\vec{r}}$ and $\Delta{t}$ are finite quantities as described in my book.

$\vec{F}\cdot\Delta{\vec{r}}=\Delta W$ is only an approximation for small changes. In general, the direction of the force may change along the way. It is only exact if the direction of F is constant.
Taking the limit produces the integral and renders the equation exact.

 

[ThEmptyTree]

I wrote that your version omitted the delta, not that you were responsible for the omission.

$\vec{F}\cdot\Delta{\vec{r}}=\Delta W$ is only an approximation for small changes. In general, the direction of the force may change along the way. It is only exact if the direction of F is constant.
Taking the limit produces the integral and renders the equation exact.

Exactly, so after all the formula $P_{ave}=\vec{F}\cdot\vec{V_{ave}}$ only works for constant direction. This is what intrigued me, because they did not specify it. Thanks.

(This is somewhat explainable because at the level of the book students are not supposed to know calculus so nor how to deal with non uniform paths, but I just wanted to make sure)

 

[haruspex]

Exactly, so after all the formula $P_{ave}=\vec{F}\cdot\vec{V_{ave}}$ only works for constant direction.

If applying it over an extended period (and displacement), if the force varies at all (not just in direction) then it is unclear what F to use.

 

[Orodruin]

When the potential is increasing (positive derivative) the force is negative (points to the left) and when the potential is decereasing (negative derivative) the force is positive (points to the right).

Is this the case for your result above?

 

[ThEmptyTree]

Is this the case for your result above?

Umm.. I think so, maybe?

 

[Orodruin]

Umm.. I think so, maybe?

What is the sign of your force when x>0?

 

[ThEmptyTree]

What is the sign of your force when x>0?

Negative, the function is increasing?

EDIT: OH F**K I FORGOT THE -

Thanks for noticing.

How can I edit the post tho?