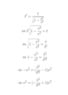Express Velocity in Formula: Find Answer

[hugo_faurand]

Hello everyone.
This is not an homework but I'd like to express velocity $v$ in this formula :
$$t' = \frac{t}{\sqrt{1-\frac{v^2}{c^2}}} $$
I've found
$$ v^2 = -(\frac{t^2}{t'^2}+1)c^2 $$

I'm sure that is wrong but I don't manage to express $v$ and find the correct answer.
Thanks in advance.

 

[berkeman]

The 2nd equation looks to be close, with just one sign error. Can you show the steps you are trying to isolate v in the first equation?

 

[hugo_faurand]

The 2nd equation looks to be close, with just one sign error. Can you show the steps you are trying to isolate v in the first equation?

If it's a problem with a sign maybe this is correct :

 

[berkeman]

If it's a problem with a sign maybe this is correct :
View attachment 227952

Yes, that looks fixed now, good work! What equation editor are you using BTW?

 

[hugo_faurand]

Yes, that looks fixed now, good work! What equation editor are you using BTW?

Yes, it works ! So finally we have :
$$v = \sqrt{(-\frac{t^2}{t'^2}+1)c^2}$$
Othewise I use ShareLaTex https://fr.sharelatex.com/ . Sorry, I'm french so it's the french version.

 

[berkeman]

I'm french

Congrats on making the World Cup finals!

 

[Janus]

Yes, it works ! So finally we have :
$$v = \sqrt{(-\frac{t^2}{t'^2}+1)c^2}$$
Othewise I use ShareLaTex https://fr.sharelatex.com/ . Sorry, I'm french so it's the french version.

Okay. So now you have c² as a factor under the radical sign. Do you see a way to reduce this down further? And do you see a way of making the other part under the radical look cleaner?

 

[hugo_faurand]

Okay. So now you have c² as a factor under the radical sign. Do you see a way to reduce this down further? And do you see a way of making the other part under the radical look cleaner?

In the radical we multiply by c^2 so we can just multiply the square root by c :
$$v = c\sqrt{(-\frac{t^2}{t'^2}+1)}$$
Also, dividing by a number is like multiplying by the inverse. So, I think we can have something like that :
$$v = c\sqrt{-{t^2}{t'^2}+1}$$

 

[Ibix]

In the radical we multiply by c^2 so we can just multiply the square root by c :

Correct (although you'd normally phrase it as "take out a factor of c outside the square root", or something like that).

$$v = c^2\sqrt{(-\frac{t^2}{t'^2}+1)}$$

So this isn't right.

Also, dividing by a number is like multiply by the inverse. So, I think we can have something like that :
$$v = c^2\sqrt{-{t^2}{t'^2}+1}$$

Only if you define $t'=1/t'$, which is a bit confusing. You could define something like $f'=1/t'$, then use that. It's not a standard usage, though.

 

[Janus]

In the radical we multiply by c^2 so we can just multiply the square root by c :
$$v = c^2\sqrt{(-\frac{t^2}{t'^2}+1)}$$
Also, dividing by a number is like multiply by the inverse. So, I think we can have something like that :
$$v = c^2\sqrt{-{t^2}{t'^2}+1}$$

Ibex already pointed out that there is an error in your first equation.
For the second part, I was thinking more along the lines of what happens when you reverse the order of the terms.

 

[hugo_faurand]

Ibex already pointed out that there is an error in your first equation.
For the second part, I was thinking more along the lines of what happens when you reverse the order of the terms.

Reverse the order of the terms ? Maybe you mean put +1 before $-\frac{t^2}{t'^2}$
So we have :
$$ v = c\sqrt{1-\frac{t^2}{t'^2}}$$

 

[Janus]

Reverse the order of the terms ? Maybe you mean put +1 before $-\frac{t^2}{t'^2}$
So we have :
$$ v = c\sqrt{1-\frac{t^2}{t'^2}}$$

Right, Now consider that at times it is more convenient to work with velocities as expressed as a fraction of c such that $\beta = \frac{v}{c}$
so how would you express this equation using $\beta$ ?

 

[hugo_faurand]

Right, Now consider that at times it is more convenient to work with velocities as expressed as a fraction of c such that $\beta = \frac{v}{c}$
so how would you express this equation using $\beta$ ?

So we have :
$$ \beta = \sqrt{1-\frac{t^2}{t'^2}}$$

 

[Janus]

So does the right hand side of the equation remind you of anything?

 

[hugo_faurand]

So does the right hand side of the equation remind you of anything?

It looks like what we have in the initial equation :
$$ \sqrt{1-\frac{v^2}{c^2}}$$

But we change $v$ and $c$ .

 

[Janus]

It looks like what we have in the initial equation :
$$ \sqrt{1-\frac{v^2}{c^2}}$$

But we change $v$ and $c$ .

Right, so if we take $\frac{t^2}{t'^2}$ and express it as $\left ( \frac{t}{t'} \right )^2$

We get
$$\beta = \sqrt{1- \left ( \frac{t}{t'} \right )^2} $$

and
$$ \frac{t}{t'} = \sqrt{1- \beta^2} $$