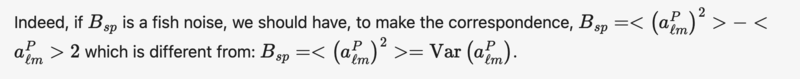fab13
- 300
- 7
- TL;DR Summary
- I would like to prove that Shot noise follows a Poisson distribution.
I would like to arrive at the following expression for the quantity ##o_{\ell}## ( with "DM" for Dark Matter ):
##o_{\ell}=b_{s p}^2 C_{\ell}^{D M}+B_{s p}##
with Poisson noise ##B_{s p}=\frac{1}{\bar{n}}(\bar{n}## being the average number of galaxies observed). the index "sp" is for spectro. I think for now that ##B_{s p}## is the variance of a Poisson noise but see the following below to really confirm: To arrive at this same expression, I would like to start from ##{ }_{\ell m}^{a D M}## (DM for Dark matter) and ##a_{\ell m}^P## (" ##\mathrm{P}## " for fish).
So I start from the fact that ##C_{\ell}=\operatorname{Var}\left(a_{\ell m}\right)## :
##o_{\ell}=<\left(b_{s p} a_{\ell m}^{D M}+a_{\ell m}^P\right)^2>##
If we expand, we have: ##o_{\ell}=<b_{s p}^2\left(a_{\ell m}^{D M}\right)^2+2 b_{s p} a_{\ell m}^{D M}+\left(a_{\ell m}^P\right)^2>##
##o_{\ell}=b_{s p}^2 C_{\ell}^{D M}+2 b_{s p}<a_{\ell m}^{D M}><a_{\ell m}^P>+<\left(a_{\ell m}^P\right)^2>##
##=b_{s p}^2 C_{\ell}^{D M}+<\left(a_{\ell m}^P\right)^2>##
because we have ##<a_{\ell_m}^{D M}>=0##
The problem comes from the term ##<\left(a_{\ell m}^P\right)^2>## : I don't know how to justify that this term is equal to ##\frac{1}{\bar{n}}##
Indeed, if ##B_{s p}## is a fish noise, we should have, to make the correspondence, ##B_{s p}=<\left(a_{\ell m}^P\right)^2>-<## ##a_{\ell m}^P>2## which is different from: ##B_{s p}=<\left(a_{\ell m}^P\right)^2>=\operatorname{Var}\left(a_{\ell m}^P\right)##.
How to obtain the quantity ##B_{s p}## which seems a priori equal to ##\frac{1}{\bar{n}}## ?
If ##B_{s p}## is equal to ##<\left(a_{\ell m}^P\right)^2>##, how to make the link with a variance since a Poisson law is not centered ( I mean ##<a_{\ell m}^P>\neq 0## ?
##o_{\ell}=b_{s p}^2 C_{\ell}^{D M}+B_{s p}##
with Poisson noise ##B_{s p}=\frac{1}{\bar{n}}(\bar{n}## being the average number of galaxies observed). the index "sp" is for spectro. I think for now that ##B_{s p}## is the variance of a Poisson noise but see the following below to really confirm: To arrive at this same expression, I would like to start from ##{ }_{\ell m}^{a D M}## (DM for Dark matter) and ##a_{\ell m}^P## (" ##\mathrm{P}## " for fish).
So I start from the fact that ##C_{\ell}=\operatorname{Var}\left(a_{\ell m}\right)## :
##o_{\ell}=<\left(b_{s p} a_{\ell m}^{D M}+a_{\ell m}^P\right)^2>##
If we expand, we have: ##o_{\ell}=<b_{s p}^2\left(a_{\ell m}^{D M}\right)^2+2 b_{s p} a_{\ell m}^{D M}+\left(a_{\ell m}^P\right)^2>##
##o_{\ell}=b_{s p}^2 C_{\ell}^{D M}+2 b_{s p}<a_{\ell m}^{D M}><a_{\ell m}^P>+<\left(a_{\ell m}^P\right)^2>##
##=b_{s p}^2 C_{\ell}^{D M}+<\left(a_{\ell m}^P\right)^2>##
because we have ##<a_{\ell_m}^{D M}>=0##
The problem comes from the term ##<\left(a_{\ell m}^P\right)^2>## : I don't know how to justify that this term is equal to ##\frac{1}{\bar{n}}##
Indeed, if ##B_{s p}## is a fish noise, we should have, to make the correspondence, ##B_{s p}=<\left(a_{\ell m}^P\right)^2>-<## ##a_{\ell m}^P>2## which is different from: ##B_{s p}=<\left(a_{\ell m}^P\right)^2>=\operatorname{Var}\left(a_{\ell m}^P\right)##.
How to obtain the quantity ##B_{s p}## which seems a priori equal to ##\frac{1}{\bar{n}}## ?
If ##B_{s p}## is equal to ##<\left(a_{\ell m}^P\right)^2>##, how to make the link with a variance since a Poisson law is not centered ( I mean ##<a_{\ell m}^P>\neq 0## ?
Last edited: