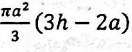Factoring Fractions: Simplifying Equations with Cancellation

  • Context:
  • Thread starter Thread starter mathlearn
  • Start date Start date
Join the discussion
Ask a follow-up here, or get your own question answered by working scientists, mathematicians and engineers — people, not an autocomplete.
Real named experts · corrections over time · the nuance an AI answer skips
Sign up Log in
9 replies · 2K views
mathlearn
Messages
331
Reaction score
0
Hi , So far I am stuck in this math problem and

View attachment 5779 MINUS (-) View attachment 5780

Subtract the first sum with pie from the second sum and you should factor it such that the a similar out come in the below given image.


Can anyone subtract and factor this for me such that View attachment 5778

and can you explain me how you did this in a little descriptive manner

Many thanks
 

Attachments

  • Capture.PNG
    Capture.PNG
    2.4 KB · Views: 145
  • Capture1.PNG
    Capture1.PNG
    618 bytes · Views: 142
  • Capture2.PNG
    Capture2.PNG
    754 bytes · Views: 130
Last edited:
Mathematics news on Phys.org
Get a common denominator and then factor.
 
I'm sorry would you be kind enough to demonstrate please!
 
$$\pi a^2h-\frac23\pi a^3=\frac{\pi a^2}{3}\cdot3h-\frac{\pi a^2}{3}{2a}=\frac{\pi a^2}{3}(3h-2a).$$
 
Thank you , can you explain a little bit on how did you solved this problem.

Many Thanks
 
mathlearn said:
can you explain a little bit on how did you solved this problem.
If you are asking how one comes up with the exact sequence of expressions $E_1,\dots,E_n$ such that $\pi a^2h-\dfrac23\pi a^3=E_1\dots=E_n=\dfrac{\pi a^2}{3}(3h-2a)$, it becomes quite obvious after some practice. If you are asking about a specific equality or transition that you don't understand in my solution, please say which one.
 
Where did /3 come from in the second step & can you explain a little step by step in doing this
 
I am using the following laws:
\begin{align}
&(1)\quad x\cdot1=x\\
&(2)\quad\dfrac{3}{3}=1\\
&(3)\quad x\dfrac{y}{z}=\dfrac{xy}{z}\\
&(4)\quad xy=yx\\
&(5)\quad (xy)z=x(yz).
\end{align}

So
\[
\pi a^2h\overset{(1)}{=}\pi a^2h\cdot1\overset{(2)}{=}\pi a^2h\cdot\dfrac33\overset{(3)}{=}\frac{\pi a^2h\cdot3}{3}\overset{(4,5)}{=}\frac{(\pi a^2)(3h)}{3}
\overset{(3)}{=}\frac{\pi a^2h}{3}\cdot 3h.
\]
 
Many thanks,
Can I know the name of the method you used to solve this
for example like quadratic equations or so
 
As I said, this is much easier than the quadratic formula and becomes obvious after some practice. The transformations used here can be called "multiplying and dividing by the same number" or "cancellation" (3 in the numerator cancels with 3 in the denominator).

It may be good to get a cheat sheet of laws of fractions, such as this one.