- #1
fab13
- 318
- 6
I am currently coding a small application that reproduces the transport of a vector along a geodesic on a 2D sphere.
Here's a capture of this application :
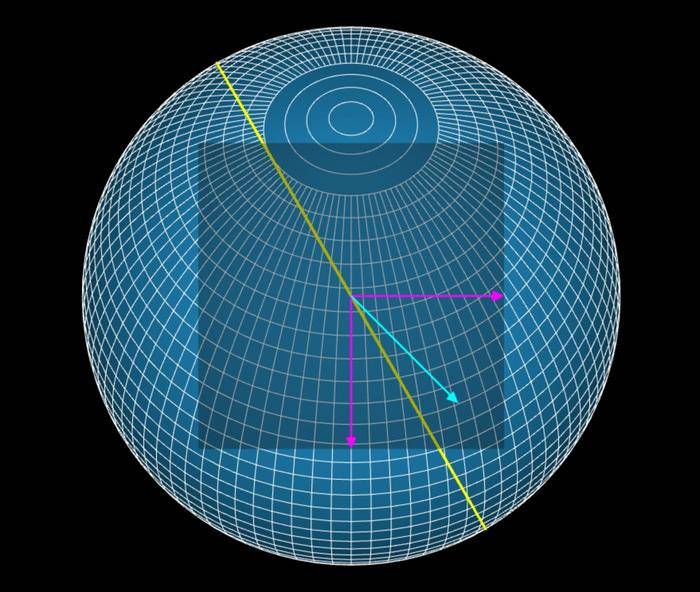
You can see as pink vectors the vectors of curvilinear coordinates and in cyan the transported vector.
The transport of vector along the geodesic (in yellow) is well reproduced from algorithmic and geometric point of view (with the using of Matrix rotation and angles computation).
Now I would like to check the validity of this transport from an analytical point of view with the equations of transport on geodesic.
For this, I am using the equations deduced from the definition of parallel transport :
$$\text{d}v^{\theta} = v^{\varphi}\sin\theta\,\cos\theta\,\text{d}\varphi\quad\quad (1)$$
and
$$\text{d}v^{\varphi} = -\cot\theta\,(v^{\theta}\text{d}\varphi + v^{\varphi}\text{d}\theta)\quad\quad (2)$$
In my simulation, I take as a convention that ##e_{\theta}## and ##e_{\varphi}## have a " norm equal to 1 ", so I can write the vector transported like :
$$\vec{V}=V^{\theta}\,\vec{e_{\theta}}+V^{\varphi}\,\vec{e_{\varphi}}$$
and take : $$||\vec{e_{\theta}}|| = 1$$ and $$||\vec{e_{\varphi}}|| = 1$$
Actually, I wonder if i have to apply factors and if yes, how to apply them (on equations above (1) and (2)). I speak about the factors that come from the definition of curvilinear basis vectors, i.e with Einstein notation :
$$\text{d}\vec{OM}=\dfrac{\partial\vec{OM}}{\partial y^{i}}\text{d}y^{i}$$
with the curvilinear basis vector ##\vec{e_{i}}= \dfrac{\partial\vec{OM}}{\partial y^{i}}##
So, with this definition, I get for ##(\vec{e_{\theta}},\vec{e_{\varphi}})##, starting from :
$$\vec{OM}=r\sin(\theta)\cos(\varphi)\vec{e_{x}}+r\sin(\theta)\sin(\varphi)\vec{e_{y}}+r\cos(\theta)\vec{e_{z}}$$
$$\vec{e_{\theta}}=r\cos(\theta)\cos(\varphi)\vec{e_{x}}+r\cos(\theta)\sin(\varphi)\vec{e_{y}}-r\sin(\theta)\vec{e_{z}}$$
$$\vec{e_{\varphi}}=-r\sin(\theta)\sin(\varphi)\vec{e_{x}}+r\sin(\theta)\cos(\varphi)\vec{e_{y}}$$
So the norms are equal to :
$$||\vec{e_{\theta}}|| = r$$ and $$||\vec{e_{\varphi}}|| = r\sin(\theta)$$
How to make the link between above norms of ##(\vec{e_{\theta}},\vec{e_{\varphi}})## and the coordinates that I am using in my code :
I mean, if it is necessary, how to apply these factors on equation `(1)` and `(2)` and mainly on which terms (##\text{d}v^{\theta}, \text{d}v^{\varphi}, v^{\theta}, v^{\varphi}##) ?
I show you below the results that I get, the first figure (FIGURE 2) represents ##\theta## and ##\varphi## during the transport and the second one (FIGURE 3) represents the total differential ##Dv^{\theta}## and ##Dv^{\varphi}## for small ##\delta## values (interval between 2 discrete values), i.e the following relations (3) and (4) :
$$\delta v^{\theta} - v^{\varphi}\sin\theta\,\cos\theta\,\delta\varphi=0\quad\quad (3)$$
with $$v^{\varphi}=v^{\varphi}_{i}$$
$$\delta v^{\theta} = v^{\theta}_{i+1}-v^{\theta}_{i}$$
$$\delta\varphi=\varphi_{i+1}-\varphi_{i}$$
$$\theta = \theta_{i}$$
and
$$\delta v^{\varphi} + \cot\theta\,(v^{\theta}\delta\varphi + v^{\varphi}\delta\theta)=0\quad\quad (4)$$
with $$v^{\varphi}=v^{\varphi}_{i}$$
$$v^{\theta}=v^{\theta}_{i}$$
$$\delta v^{\varphi} = v^{\varphi}_{i+1}-v^{\varphi}_{i}$$
$$\delta\varphi=\varphi_{i+1}-\varphi_{i}$$
$$\delta\theta=\theta_{i+1}-\theta_{i}$$
$$\theta = \theta_{i}$$
These 2 relations (3) and (4) must be equal to zero. I have taken a transported vector of norm equal roughly to `20`.
FIGURE 2 :
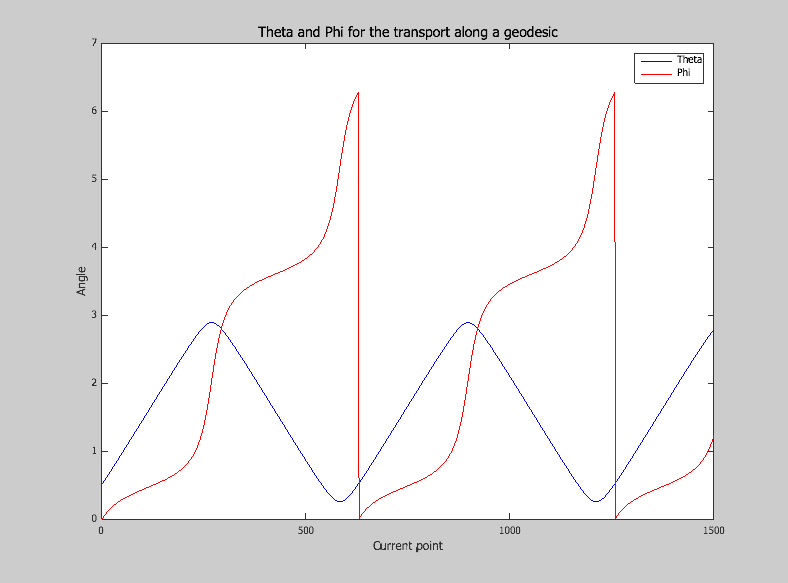
FIGURE 3 :
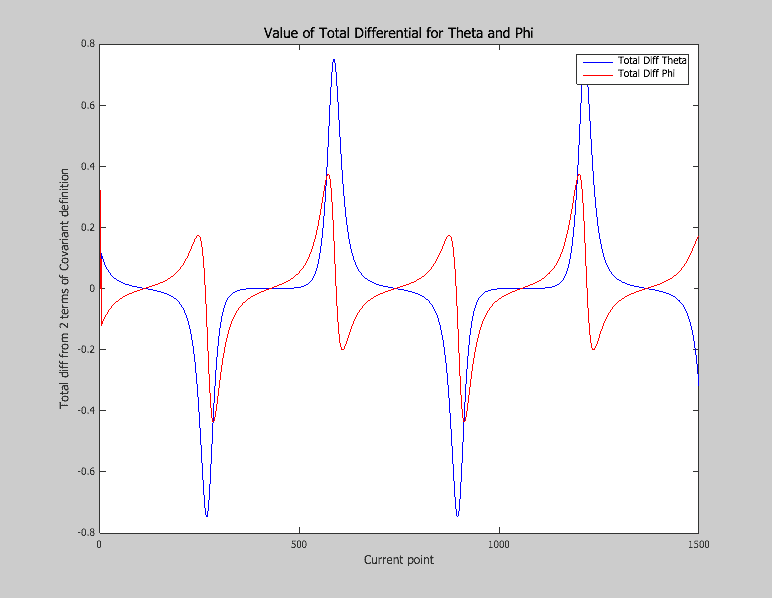
As you can on figure 3, I don't get values near to zero, the biggest shift is equal roughly to +-0.7 for ##Dv^{\theta}## and +-0.4 for ##Dv^{\varphi}## (with a transported vector of norm equal to 20).
Do you think these results are consistent with theoretical expectations ? and should I apply factors that I specified at the begin of this thread.
Thanks for your help
Here's a capture of this application :
You can see as pink vectors the vectors of curvilinear coordinates and in cyan the transported vector.
The transport of vector along the geodesic (in yellow) is well reproduced from algorithmic and geometric point of view (with the using of Matrix rotation and angles computation).
Now I would like to check the validity of this transport from an analytical point of view with the equations of transport on geodesic.
For this, I am using the equations deduced from the definition of parallel transport :
$$\text{d}v^{\theta} = v^{\varphi}\sin\theta\,\cos\theta\,\text{d}\varphi\quad\quad (1)$$
and
$$\text{d}v^{\varphi} = -\cot\theta\,(v^{\theta}\text{d}\varphi + v^{\varphi}\text{d}\theta)\quad\quad (2)$$
In my simulation, I take as a convention that ##e_{\theta}## and ##e_{\varphi}## have a " norm equal to 1 ", so I can write the vector transported like :
$$\vec{V}=V^{\theta}\,\vec{e_{\theta}}+V^{\varphi}\,\vec{e_{\varphi}}$$
and take : $$||\vec{e_{\theta}}|| = 1$$ and $$||\vec{e_{\varphi}}|| = 1$$
Actually, I wonder if i have to apply factors and if yes, how to apply them (on equations above (1) and (2)). I speak about the factors that come from the definition of curvilinear basis vectors, i.e with Einstein notation :
$$\text{d}\vec{OM}=\dfrac{\partial\vec{OM}}{\partial y^{i}}\text{d}y^{i}$$
with the curvilinear basis vector ##\vec{e_{i}}= \dfrac{\partial\vec{OM}}{\partial y^{i}}##
So, with this definition, I get for ##(\vec{e_{\theta}},\vec{e_{\varphi}})##, starting from :
$$\vec{OM}=r\sin(\theta)\cos(\varphi)\vec{e_{x}}+r\sin(\theta)\sin(\varphi)\vec{e_{y}}+r\cos(\theta)\vec{e_{z}}$$
$$\vec{e_{\theta}}=r\cos(\theta)\cos(\varphi)\vec{e_{x}}+r\cos(\theta)\sin(\varphi)\vec{e_{y}}-r\sin(\theta)\vec{e_{z}}$$
$$\vec{e_{\varphi}}=-r\sin(\theta)\sin(\varphi)\vec{e_{x}}+r\sin(\theta)\cos(\varphi)\vec{e_{y}}$$
So the norms are equal to :
$$||\vec{e_{\theta}}|| = r$$ and $$||\vec{e_{\varphi}}|| = r\sin(\theta)$$
How to make the link between above norms of ##(\vec{e_{\theta}},\vec{e_{\varphi}})## and the coordinates that I am using in my code :
I mean, if it is necessary, how to apply these factors on equation `(1)` and `(2)` and mainly on which terms (##\text{d}v^{\theta}, \text{d}v^{\varphi}, v^{\theta}, v^{\varphi}##) ?
I show you below the results that I get, the first figure (FIGURE 2) represents ##\theta## and ##\varphi## during the transport and the second one (FIGURE 3) represents the total differential ##Dv^{\theta}## and ##Dv^{\varphi}## for small ##\delta## values (interval between 2 discrete values), i.e the following relations (3) and (4) :
$$\delta v^{\theta} - v^{\varphi}\sin\theta\,\cos\theta\,\delta\varphi=0\quad\quad (3)$$
with $$v^{\varphi}=v^{\varphi}_{i}$$
$$\delta v^{\theta} = v^{\theta}_{i+1}-v^{\theta}_{i}$$
$$\delta\varphi=\varphi_{i+1}-\varphi_{i}$$
$$\theta = \theta_{i}$$
and
$$\delta v^{\varphi} + \cot\theta\,(v^{\theta}\delta\varphi + v^{\varphi}\delta\theta)=0\quad\quad (4)$$
with $$v^{\varphi}=v^{\varphi}_{i}$$
$$v^{\theta}=v^{\theta}_{i}$$
$$\delta v^{\varphi} = v^{\varphi}_{i+1}-v^{\varphi}_{i}$$
$$\delta\varphi=\varphi_{i+1}-\varphi_{i}$$
$$\delta\theta=\theta_{i+1}-\theta_{i}$$
$$\theta = \theta_{i}$$
These 2 relations (3) and (4) must be equal to zero. I have taken a transported vector of norm equal roughly to `20`.
FIGURE 2 :
FIGURE 3 :
As you can on figure 3, I don't get values near to zero, the biggest shift is equal roughly to +-0.7 for ##Dv^{\theta}## and +-0.4 for ##Dv^{\varphi}## (with a transported vector of norm equal to 20).
Do you think these results are consistent with theoretical expectations ? and should I apply factors that I specified at the begin of this thread.
Thanks for your help