Fallin' staR's question at Yahoo Answers regarding kinematics

[MarkFL]

Here is the question:

Maths Prob5: Velocity & Acceleration?

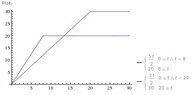
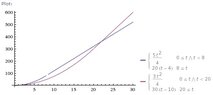
A motorbike and a car are waiting side by side at traffic lights, when the lights turn to green, the motorbike accelerates at a 2.5 m/s² up to a top speed of 20 m/s, and the car accelerates at 1.5 m/s² up to a top speed of 30 m/s . Both then continue to move at constant speed. Draw (t,v) graphs for each vehicle, using the same axes, and sketch the (t,s) graphs.

(a) after what time will the motorbike and the car again be side by side?
(b) what is the greatest distance that the motorbike is in front of the car?

No need to show the Graphs, BUT I do want to know how to draw Displacement-time Graph when the object accelerates up to a point and then moves in a constant velocity, maybe accelerated part is curve line ?!

ANSWERS: (a) 22s (b) 53.3m

#Mechanics #A-Level

HELP!

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello Fallin' staR,

We will let $a(t)$ be acceleration, $v(t)$ be velocity, and $s(t)$ be position, and use a subscript of $\text{M}$ for the motorbike and a subscript of $\text{C}$ for the car.

For the motorbike, during the time its acceleration is greater than zero, that is, when its velocity is changing, we may state:

\(\displaystyle \int_0^{v(t)}\,du=\frac{5}{2}\int_0^t\,dw\)

\(\displaystyle v(t)=\frac{5}{2}t\)

Now, we need to find at what value of $t$ we have $v(t)=20$, thus:

\(\displaystyle 20=\frac{5}{2}t\)

Solve for $t$:

\(\displaystyle t=8\)

And so we may now give the velocity of the motorbike as:

\(\displaystyle v_{\text{M}}(t)=\begin{cases}\frac{5}{2}t & t<8\\ 20 & 8\le t \\ \end{cases}\)

For the car, during the time its acceleration is greater than zero, that is, when its velocity is changing, we may state:

\(\displaystyle \int_0^{v(t)}\,du=\frac{3}{2}\int_0^t\,dw\)

\(\displaystyle v(t)=\frac{3}{2}t\)

Now, we need to find at what value of $t$ we have $v(t)=30$, thus:

\(\displaystyle 30=\frac{3}{2}t\)

Solve for $t$:

\(\displaystyle t=20\)

And so we may now give the velocity of the car as:

\(\displaystyle v_{\text{C}}(t)=\begin{cases}\frac{3}{2}t & t<20\\ 30 & 20\le t \\ \end{cases}\)

Here is a plot of the two velocity functions on the same axes:

View attachment 1234

To generate this graph, I used the command:

piecewise[{{(5/2)t,0<=t<8},{20,8<=t}}],piecewise[{{(3/2)t,0<=t<20},{30,20<=t}}] where t=0 to 30

at Wolfram|Alpha: Computational Knowledge Engine

Now, to find the position function of the motorbike, we may use:

On the interval $0\le t<8$:

\(\displaystyle \int_0^{s(t)}\,du=\frac{5}{2}\int_0^{t} w\,dw\)

\(\displaystyle s(t)=\frac{5}{4}t^2\)

We will need to know that:

\(\displaystyle s(8)=80\)

On the interval $8\le t$:

\(\displaystyle \int_{s(8)}^{s(t)}\,du=20\int_8^t \,dw\)

\(\displaystyle s(t)=20t-80\)

Thus, we may state:

\(\displaystyle s_{\text{M}}(t)=\begin{cases}\frac{5}{4}t^2 & t<8\\ 20t-80 & 8\le t \\ \end{cases}\)

Now, to find the position function of the car, we may use:

On the interval $0\le t<20$:

\(\displaystyle \int_0^{s(t)}\,du=\frac{3}{2}\int_0^t w\,dw\)

\(\displaystyle s(t)=\frac{3}{4}t^2\)

We will need to know that:

\(\displaystyle s(20)=300\)

On the interval $20\le t$:

\(\displaystyle \int_{s(20)}^{s(t)}\,du=30\int_{20}^t \,dw\)

\(\displaystyle s(t)=30t-300\)

Thus, we may state:

\(\displaystyle s_{\text{C}}(t)=\begin{cases}\frac{3}{4}t^2 & t<20\\ 30t-300 & 20\le t \\ \end{cases}\)

Using the command:

piecewise[{{(5/4)t^2,0<=t<8},{20t-80,8<=t}}],piecewise[{{(3/4)t^2,0<=t<20},{30t-300,20<=t}}] where t=0 to 30

we obtain the plot:

View attachment 1235

Now we may answer the two questions:

(a) after what time will the motorbike and the car again be side by side?

From the graph, we see we want to equate the two linear portions of the position functions:

\(\displaystyle 20t-80=30t-300\)

\(\displaystyle 10t=220\)

\(\displaystyle t=22\text{ s}\)

Thus, we find that the motorbike and the car are again side by side 22 seconds after the traffic light turns green.

(b) what is the greatest distance that the motorbike is in front of the car?

The graph shows us that this will occur on the interval $8<t<20$. Hence we want to maximize the function:

\(\displaystyle f(t)=\left(20t-80 \right)-\left(\frac{3}{4}t^2 \right)=-\frac{3}{4}t^2+20t-80\)

Completing the square, we find:

\(\displaystyle f(t)=-\frac{3}{4}\left(t-\frac{40}{3} \right)^2+\frac{160}{3}\)

Hence:

\(\displaystyle f_{\max}=\frac{160}{3}\text{ m}\)

And so we find the greatest distance that the motorbike is in front of the car to be about 53.3 m.