Faraday's Nested Sphere Experiment

[BlackMelon]

Hi there!

I have a question about the Faraday's Nested Sphere Experiment, please see the attached pdf. I wonder why equation (1) and the electric field's equation ( coming after (1) ) consider only the charge Q. Why there aren't charge -Q in the equation?

Ps. I'm thinking about point charges. When you have two charges: +Q and -Q, and you want to find the electric field at point x. You need to put both +Q and -Q in an equation:

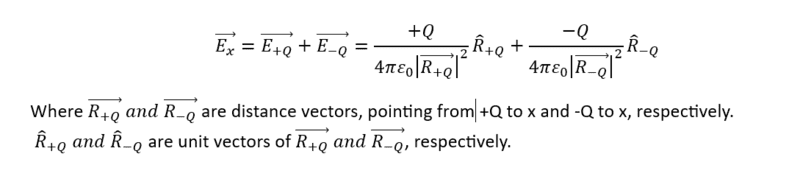
BlackMelon

 

[hutchphd]

Because the flux density is radially outward for both (via Gauss's law) . For the outer shell this is into the local surface of the outer shell.
It is true that there needs to be -Q on the inside of the outer shell to kill the field inside the outer conductor. Thus +Q is left on the outside of the outer conductor before it is grounded.

 

[BlackMelon]

About the Gauss's law, could you take a look at the file inside the link below?

SITUATION 1:
There were positive charges at the outer surface of the outer shell. As we connect the ground, the outer surface becomes neutral.
Afterwards, I define the gaussian surface (dotted line). The magnitude of electric field at each point normal to the gaussian surface is E1.

SITUATION2:
This experiment has only the same charge +Q and the same gaussian surface. No other instruments.
The magnitude of electric field is E2.

Is E1 > E2?
From the bottom most picture, I inspect the two negative charges (blue one and green one) and their effects on the Gaussian surface (red circle). At x, the blue one will add up with the field from the positive charge. The green one will deduct the field, but its effect is lesser, since it is far away from x. So in total, the field coming out of x will be more than that in the situation 2. Am I correct?

BlackMelon

The attached picture resolution is not good. Take this link:
https://www.mediafire.com/file/npoqe0qaekziezs/Gaussian1.jpg/file

 

[vanhees71]

I don't know, if it is so helpful to use such hand-waving arguments. Rather one should analyze the problem, using the electrostatic Maxwell equations. Since the problem is spherically symmetric, it's clear that the em. field everywhere has the form of a Coulomb field
$$\vec{E}=\frac{q}{4 \pi \epsilon_0 r^3} \vec{r}.$$
For the grounded outer sphere you have the outer surface at equal potential $0$, and thus outside the outer surface the field is $0$. This implies that at the inner surface of the outer spherical shell must be a total charge $-Q$.

If you have the situation before grounding the outer sphere, then the total charge on both its inner and outer surface must be 0, because it was 0 before putting it around the inner sphere, and no net-charge has been in any way transported from or to the outer sphere. This is achieved by simply putting a total charge $+Q$ on the outer surface of the outer shell compared to the situation when the outer sphere is grounded. Thus in this case you have outside again the Coulomb field with $q=+Q$.