[FDTD/FORTRAN] problem with tfsf boundary and berenger's pml

  • Thread starter s_hy
  • Start date
  • Tags
    Boundary
In summary, the conversation discusses a code written for 2D FDTD TFSF with Berenger's PML absorbing boundary condition. The issue of serious leakage at the front and right boundaries is mentioned, and it is determined that the problem may be coming from the TFSF boundary or the absorbing boundary condition. The code and output are also attached for reference. The conversation also includes details about the model size, TFSF boundary, and initialization for incident and field evolution. Additionally, the use of Berenger's ABC PML is explained, along with the setup for the PML absorbing boundaries and the initialization of various matrices.
  • #1
s_hy
61
0
hi all...

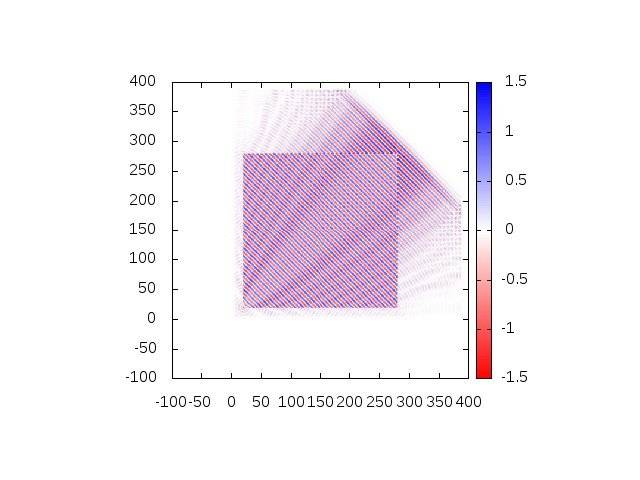
I have written codes for 2d fdtd tfsf with berenger's pml absorbing boundary. But I have serious leakage at front and right boundary. At the first place I think the problem is because the pml, but pml is working perfectly in the left and bottom boundary. I need an advice whether the problem is coming from tfsf boundary or absorbing boundary condition. Attached here is my code as well as output produced.

Code: 
module data_module
implicit none

integer                                         :: i,j,k,ie,je,ia,ib,ja,jb,hinit,hlast, n,nt,m0,iinit,jinit
double precision,parameter     :: f0 = 3.0e7,c = 3.e8,eps0 = 8.8e-12,pi  = 3.14159,miu0 = 4*pi*1e-7
double precision,parameter     :: s = -0.477369,p = -1.0/3.0,q = -miu0*c/6,r = -miu0*c/2               ! mur absorbing boundary condition
double precision,parameter     :: lamda = c/f0,dx = lamda/10,dt = dx/(6e8)
double precision,parameter     :: A0 = 1.0
double precision,parameter     :: Cb = 1/(2*eps0*c),Db = 1/(2*miu0*c)
double precision                        :: epsr,miur,phi,cosphi,sinphi
double precision,dimension(-10:1000)               :: Einc0,Einc1,Hinc0
double precision,dimension(1000,1000)             :: Ez,Hy,Hx
double precision,dimension(1000,1000)             :: Ez1,Ez2,Ez3,Ez4,Ez0
double precision,dimension(-10:1000,-10:1000) :: Ezinc,Hxinc,Hyinc
double precision,dimension(1000,1000)             :: Cax,Cbx,Dax,Dbx
double precision,dimension(1000,1000)             :: miu,eps,sigma, sigmat
character(len=20)                                                 :: filename
  
 end module data_module
 
! #################################################################################################
subroutine  tfsfpml
use data_module
implicit none


integer                    :: npml,m,ip,jp
double precision    :: smax,rmax,imp               ! sigma max, rho max, impedance
double precision    :: t,d,dp
double precision    :: re,rm
double precision,dimension (500)    :: ga,gb,ha,hb,sig,rho
 
 phi = pi/4
 cosphi = cos(phi)
 sinphi = sin(phi)
 m0 = 1
 
! model size
 ie = 400
 je = 400 
 hinit = -10
 hlast = 500
 iinit = 1
 jinit = 1
 
 ! tfsf boundary
 !ia = ie/4
 !ja = je/4
 !ib = ie*3/4
 !jb = ib
 ia = 20
 ja = 20
 ib = 280
 jb = 280
 
! initialization for incident wave
  Hinc0 = 0
  Einc0 = 0
   
! initialization for field evolution
   Hx = 0
   Hy = 0
   Ez = 0
   Ez1 = 0
   Ez2 = 0
   Ez3 = complex(0.0,0.0)
   Ez4 = 0
   
! :::::::::::::::::BERENGER'S ABC PML:::::::::::::::::::::::::::::::::::::::::::   
! set up for berenger pml abc material
 npml = 10
 ip = ie - npml
 jp = je - npml

 imp = sqrt(miu0/eps0)
 smax = -3.0*eps0*c*log(1e-5)/(2.0*dx*npml)
 rmax = smax*(imp**2)

 do m = 1,npml
   sig(m)=smax*((m-0.5)/(npml+0.5))**2
   rho(m)=rmax*(m/(npml+0.5))**2
 end do
 
 ! set up constant needed in fdtd equations
 do m = 1,npml+5
   re = sig(m)*dt/eps0
   rm = rho(m)*dt/miu0
   ga(m) = exp(-re)
   gb(m) = -(exp(-re)-1.0)/sig(m)/dx
   ha(m) = exp(-rm)
   hb(m) = -(exp(-rm)-1.0)/rho(m)/dx
 end do
     
! medium's properties
 miur = 1.0
 epsr = 1.0
 
! initialize permittivity and permeability 
  do i = 1,ie
   do j = 1,je
     eps(i,j) = epsr*eps0
     miu(i,j) = miur*miu0
   end do
  end do
 
! initialize electric conductivity & magnetic conductivity
  do i = 1,ie
   do j = 1,je  
     sigma(i,j) = 0.0
     sigmat(i,j) = 0.0
     Cax(i,j) = (1.- sigma(i,j)*dt/(2.*eps(i,j)))/(1. + (sigma(i, j)*dt)/(2.*eps(i,j)))
     Cbx(i,j) = (dt/(eps(i,j)*dx))/(1.+sigma(i,j)*dt/(2.*eps(i,j)))
     Dax(i,j) = (1.-sigmat(i,j)*dt/(2.*miu(i,j)))/(1. +(sigmat(i,j)*dt)/(2.*miu(i,j)))
     Dbx(i,j) = (dt/(miu(i,j)*dx))/(1. + sigmat(i,j)*dt/(2.*miu(i,j)))
     !print*, 'Cax(i,j)=',Cax(i,j),'Cbx(i,j)=',Cbx(i,j),'Dax(i,j)=',Dax(i,j),'Dbx(i,j)=',Dbx(i,j)
   end do
  end do

!::::: initialize all of the matrices for the Berenger pml absorbing boundaries ::::::::::::::
! Ez field - left and right pml regions
 do i = 2,ie+50
   do  j = 2,npml
      m = npml + 2 - j
      Cax(i,j) = ga(m)
      Cbx(i,j) = gb(m)
   end do
   do j = jp-1,je+5
      m = j-jp
      Cax(i,j) = ga(m)
      Cbx(i,j) = gb(m)
    end do
  end do

! Ez field - back and front pml regions  
 do j = 2,je+50
   do i = 2,npml
      m = npml + 2 - i
      Cax(i,j) = ga(m)
      Cbx(i,j) = gb(m)
   end do
   do i = ip-1,ie+5
      m = i-ip
      Cax(i,j) = ga(m)
      Cbx(i,j) = gb(m)
  end do
 end do

! Hx field - left and right pml regions
 do i = 2,ie+50
   do j = 1,npml
      m = npml + 1-j
      Dax(i,j) = ha(m)
      Dbx(i,j) = hb(m)
   end do
   do j = jp-1,je+5
      m = j-jp
      Dax(i,j) = ha(m)
      Dbx(i,j) = hb(m)
    end do
 end do

! Hy field - back and front pml regions
 do j = 2,je+50
   do i =1,npml
      m = npml+1-i
      Dax(i,j) = ha(m)
      Dbx(i,j) = hb(m)
    end do
    do i = ip-1,ie+5
      m = i-ip
      Dax(i,j) = ha(m)
      Dbx(i,j) = hb(m)
    end do
 end do
!-------------------------------------------------------------------------------------------------------------
  
! time steps start
do n = 1,1000
  
  write (filename, "('data',I5.4,'.dat')") n
  open (unit=31,file=filename)

! incident wave  
  t = n*dt 
  Einc1 = Einc0
  
  do k = hinit,hlast
     Hinc0(k) = Hinc0(k) - Db*(Einc1(k+1)-Einc1(k))
  end do
  
  do k = hinit+1,hlast-1
    Einc0(k) = Einc1(k) - Cb*(Hinc0(k)-Hinc0(k-1))
  end do
  
  do i = ia,ib           
   do j = ja,jb
    d = cosphi*(i - ia) + sinphi*(j - ja)
    dp = d - int(d)     
    Ezinc(i,j) = (1-dp)*Einc0(m0+int(d))+dp*Einc0(m0+int(d+1))
   end do
  end do
   
  Einc0(2) = A0*sin (2*pi*f0*n*dt)
  
  k = hlast
  Einc0(k) = Einc1(k-1)-1.0/3.0*(Einc0(k-1)-Einc1(k))
  
  k = hinit
  Einc0(k) = Einc1(k+1)-1.0/3.0*(Einc0(k+1)-Einc1(k))
  
! Hxincident field 
  do i = ia,ib
     j = ja
    d = cosphi*(i-ia)+sinphi*(j-0.5-ja)+0.5
    dp = d - int(d)
    Hxinc(i,j-1) = (dp*Hinc0(m0-1+int(d)+1)+(1-dp)*Hinc0(m0-1+int(d)))*sinphi
  end do
  
  do i = ia,ib
    j = jb
    d = cosphi*(i-ia)+sinphi*(j+0.5-ja)+0.5
    dp = d - int(d)
    Hxinc(i,j) = (dp*Hinc0(m0-1+int(d)+1)+(1-dp)*Hinc0(m0-1+int(d)))*sinphi
  end do
  
! Hyincident field
 do j = ja,jb
   i = ia
   d = cosphi*(i-0.5-ia) + sinphi*(j-ja)+0.5
   dp = d - int(d)
   Hyinc(i-1,j) = ((dp*Hinc0(m0-1+int(d)+1)) + (1-dp)*Hinc0(m0-1+int(d)))*(-cosphi)
 end do
 
 do j = ja,jb
   i = ib
   d = cosphi*(i+0.5-ia) + sinphi*(j-ja)+0.5
   dp = d - int(d)
   Hyinc(i,j) = ((dp*Hinc0(m0-1+int(d)+1))+(1-dp)*Hinc0(m0-1+int(d)))*(-cosphi)
 end do
 
! update Hx field-------------------------------------------------------------------------------------------------------
 do i = 1,ie
   do j = 1,je-1
      Hx(i,j) = Hx(i,j) - Dbx(i,jb)*(Ez(i,j+1)-Ez(i,j))
   end do
 end do
 
! tfsf for hx
  do i = ia,ib
    Hx(i,ja-1) = Hx(i,ja-1) + Dbx(i,ja-1)*Ezinc(i,ja)
  end do
  
  do i = ia,ib
    Hx(i,jb+1) = Hx(i,jb+1) - Dbx(i,jb+1)*Ezinc(i,jb)
  end do
   
! update Hy field-----------------------------------------------------------------------------------------------------
  do i = 1,ie-1
    do j = 1,je
      Hy(i,j) = Hy(i,j) + Dbx(i,j)*(Ez(i+1,j)-Ez(i,j))
    end do
  end do
  
! tfsf for hy 
 do j = ja,jb
   Hy(ia-1,j) = Hy(ia-1,j) - Dbx(ia-1,j)*Ezinc(ia,j)
 end do
 
 do j = ja,jb
   Hy(ib+1,j) = Hy(ib+1,j) + Dbx(ib+1,j)*Ezinc(ib,j)
  end do
  
!  update for Ez-----------------------------------------------------------------------------------------------------------
 do i = 2, ie-1
   do j = 2,je-1
     Ez(i,j) = Cax(i,j)*Ez(i,j) + Cbx(i,j)*(Hy(i,j) - Hy(i-1,j) - Hx(i,j) + Hx(i,j-1))
     write (31,*) i,j,Ez(i,j)
     if (j == 399) write (31,*) ' ' 
   end do
 end do
 
! update tfsf for Ez
 do j = ja+1,jb-1
   Ez(ia,j) = Ez(ia,j) - Cbx(ia,j)*Hyinc(ia-1,j)
 end do
 
 do j = ja+1,jb-1
   Ez(ib,j) = Ez(ib,j) + Cbx(ib,j)*Hyinc(ib,j)
 end do
 
 do i = ia+1,ib-1
   Ez(i,ja) = Ez(i,ja) + Cbx(i,ja)*Hxinc(i,ja-1)
 end do
 
 do i = ia+1,ib-1
   Ez(i,jb) = Ez(i,jb) - Cbx(i,jb)*Hxinc(i,jb)
 end do
  
 close (unit=31)
 
 end do
 
end subroutine  tfsfpml

data0788.jpg
 
Physics news on Phys.org
  • #2
Not understanding what you're trying to do but trying to help.

Often when a program mostly works but has some problem on the fringes of data computation means that perhaps your for loop indexes are off by 1 so say you want to loop ten times because you have ten values to average but an index is off by one then you actually loop by 9 or by 11 times meaning either one number was not averaged in or some undefined number was averaged in causing strange artifacts in your data as you used the average to compute over things.

So the bottom line is check your loops to be sure they are iterating over your data correctly.
 
  • #3
You have some weird code:
Code: 
 imp = sqrt(miu0/eps0)
 smax = -3.0*eps0*c*log(1e-5)/(2.0*dx*npml)
 rmax = smax*(imp**2)

Why not the following:

Code: 
 imp = sqrt(miu0/eps0)
 smax = -3.0*eps0*c*log(1e-5)/(2.0*dx*npml)
 rmax = smax*(miu0/eps0)

Taking square roots and later squaring the result for re-use kills some of the precision of the original value.
 
  • #4
Steamking,

I have changed the weird part, but the output is still same.
 
  • #6
sorry...I expected anyone who know FDTD are familiar with term tfsf and berenger's pml because you can find it in fdtd textbook everywhere. Sorry, I will more concern about this. Thank you for your advise.

FDTD : finite difference time domain
TFSf : total field scattered field
PML : perfectly matched layer
 
  • #7
I see lots of fishy stuff, which may make problems. In defining double precision constants, why do you use "e" instead of "d"? Pi is a double precision number, but you only assign it to 3.14159. Hence, cosphi and sinphi should both be equal to sqrt(2.0d0)/2.0d0. Are they?
Always write e.g. "1.0d0" instead of "1.0", only.
 
  • #8
I am newbie in Fortran. I may mislook about these things. I noted that pi should be assigned as pi = 3.14159265358979. for double precision constant, as example c = 3e8 means that c = light velocity = 3x10**8. about cosphi and sinphi, I don't understand why did you suggested that?
 
  • #9
s_hy said:
. for double precision constant, as example c = 3e8 means that c = light velocity = 3x10**8. about cosphi and sinphi, I don't understand why did you suggested that?

I mean you should write c=3.0d8 instead of 3e8. d is for double precision numbers, e for single precision.
This cosphi and sinphi are used very often and imprecisions in pi may matter.
 

FAQ: [FDTD/FORTRAN] problem with tfsf boundary and berenger's pml

1. What is the TFSF boundary in FDTD?

The TFSF (Total Field/Scattered Field) boundary is a numerical technique used in Finite-Difference Time-Domain (FDTD) simulations to separate the total electric and magnetic fields from the scattered fields. This allows for the simulation of electromagnetic waves propagating in a medium with an incident wave source without interference from reflections at the boundaries.

2. How does the TFSF boundary work?

The TFSF boundary works by setting up a fictitious boundary in the simulation grid, where the total fields are calculated and the scattered fields are removed. This allows for the incident wave to pass through the boundary without interference, while still allowing for the calculation of the scattered fields within the simulation domain.

3. What is Berenger's PML in FDTD?

Berenger's Perfectly Matched Layer (PML) is a numerical technique used in FDTD simulations to absorb outgoing electromagnetic waves at the boundaries of the simulation domain. It is based on a complex-valued coordinate stretching in which the electromagnetic fields are attenuated, effectively eliminating reflections from the boundaries.

4. How does Berenger's PML work?

Berenger's PML works by introducing a complex-valued coordinate stretching in the simulation grid, which attenuates the outgoing electromagnetic waves and prevents reflections at the boundaries. The stretching is designed to match the impedance of the PML layer to that of the medium being simulated, effectively absorbing the waves without causing any interference.

5. What are some common problems with the TFSF boundary and Berenger's PML in FDTD simulations?

Some common problems with the TFSF boundary and Berenger's PML in FDTD simulations include the incorrect implementation of the boundary conditions, improper selection of PML parameters, and numerical instability due to the complex-valued stretching. It is important to carefully check the simulation setup and parameters to ensure the accuracy and stability of the results.

Similar threads

Fortran Need help with Jacobi relaxation method for Dirichlet boundary conditions
Replies
1
Views
1K
[FDTD/Fotran] detected reflection near boundary but don't know why
Replies
4
Views
2K
MATLAB [matlab-fortran] translate interpolation
Replies
5
Views
3K
Fortran [fortran90] having problem to call back the value from previous loop
Replies
5
Views
2K
Fortran [Fortran90] fdtd in polar coordinates, got infinity output
Replies
4
Views
3K
How to put mur's absorbing boundary condition in 1d fdtd maxwell equation
Replies
1
Views
4K
Would this have been optimized by a compiler?
Replies
3
Views
1K
Fortran Solving Large/Infinite Results w/Yee 1D FDTD Code
Replies
2
Views
1K
Fortran [Fortran90] how to write increment in dimension
Replies
4
Views
3K
Fortran [fortran90] have problem in real array index
Replies
4
Views
12K

Hot Threads

Recent Insights

Back
Top