chikchok
- 7
- 0
- TL;DR
- Fermi energy definition and fermi-dirac distribution
1)In my book , there is a definition of fermi energy as topmost filled level in the ground state of an N electron system. This definition holds only for absolute zero,right? If it is not absolute zero,fermi energy is the energy at which the probability of a state being occupied is 50 percent. Please, tell me if I am understanding this correctly.
2)I was wondering why at low temperatures Fermi-Dirac function goes sharply from 1 to 0 and for higher temperature it goes down smoothly. Is it reasonable to assume that for low temperature, levels below the fermi level are filled and all above are empty? But why it does not happen with higher temperatures. Thank you in advance.
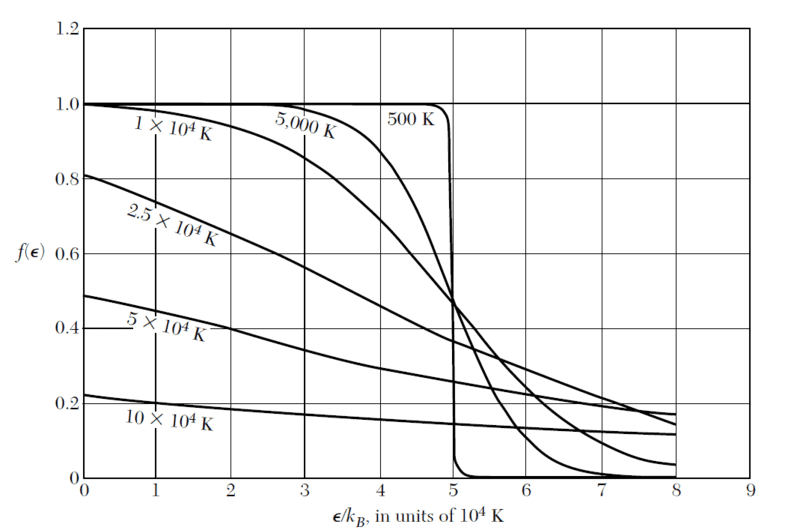
2)I was wondering why at low temperatures Fermi-Dirac function goes sharply from 1 to 0 and for higher temperature it goes down smoothly. Is it reasonable to assume that for low temperature, levels below the fermi level are filled and all above are empty? But why it does not happen with higher temperatures. Thank you in advance.
Last edited by a moderator: