Feynman rules on a ##\phi^3, \phi^4## theory

[JD_PM]

TL;DR Summary

I want to understand how Feynman rules look in a weakly coupled theory that not only has an interaction term $\phi^4$ term but also a $\phi^3$ term (please see the Lagrangian density below). To do so I am comparing it to QED's Feynman rules (which I studied from Mandl & Shaw's second edition, section 7.3).

The weakly coupled theory is given by the Lagrange density$$\mathcal{L}=\mathcal{L}_0 + \mathcal{L}_I=\frac 1 2 \partial_{\mu} \phi \partial^{\mu} \phi - \frac{m^2}{2} \phi^2 - \frac{\lambda_3}{3!} \phi^3 - \frac{\lambda_4}{4!} \phi^4 \tag{1}$$

Where

\begin{equation*}
\mathcal{L}_0 = \frac 1 2 \partial_{\mu} \phi \partial^{\mu} \phi - \frac{m^2}{2} \phi^2
\end{equation*}

\begin{equation*}
\mathcal{L}_I = - \frac{\lambda_3}{3!} \phi^3 - \frac{\lambda_4}{4!} \phi^4
\end{equation*}

My aim is to derive what are the Feynman rules for such a theory.

I could go for the brute approach; evaluating the S-matrix expansion explicitly (where I use :: for normal ordering)

\begin{align*}
S_{fi}&=\langle f | T \left\{ \exp\left( i\frac{\lambda_3}{3!}\int d^4 x :\phi (x)\phi (x)\phi (x) : + i\frac{\lambda_4}{4!}\int d^4 x :\phi (x)\phi (x)\phi (x)\phi (x) : \right) \right\}| i \rangle \\
&= \langle f | i \rangle + i \frac{\lambda_3}{3!} \int d^4 x \langle f| :\phi (x)\phi (x)\phi (x): |i \rangle + i\frac{\lambda_4}{4!} \int d^4 x \langle f | :\phi (x)\phi (x)\phi (x)\phi (x) : | i \rangle \\
&+ \left(\frac{i\lambda_3}{3!}\right)^2\frac{1}{2!} \int d^4 x d^4 y \langle f| T\left\{ : \phi (x)\phi (x)\phi (x) :: \phi (y)\phi (y)\phi (y) : \right\}|i\rangle \\
&+ \left(\frac{i\lambda_4}{4!}\right)^2\frac{1}{2!} \int d^4 x d^4 y \langle f| T\left\{ : \phi (x)\phi (x)\phi (x)\phi (x) :: \phi (y)\phi (y)\phi (y)\phi (y) \right\}: |i\rangle + \mathcal{O}(\lambda_3^4, \lambda_4^4)
\end{align*}

Before evaluating the 4 terms above, let me first make a guess

As building blocks for Feynman diagrams, we will have 2 types of interaction vertices

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$

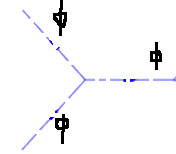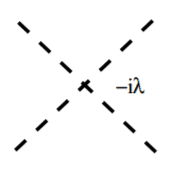
Where I followed the convention of writing mesons with dotted lines.

The left diagram comes from $i \frac{\lambda_3}{3!} \int d^4 x \langle f| :\phi (x)\phi (x)\phi (x): |i \rangle$. The right diagram comes from $i\frac{\lambda_4}{4!} \int d^4 x \langle f | :\phi (x)\phi (x)\phi (x)\phi (x) : | i \rangle$

If we were to evaluate $\left(\frac{i\lambda_3}{3!}\right)^2\frac{1}{2!} \int d^4 x d^4 y \langle f| T\left\{ : \phi (x)\phi (x)\phi (x) :: \phi (y)\phi (y)\phi (y) : \right\}|i\rangle$ we would end up getting meson scattering i.e.

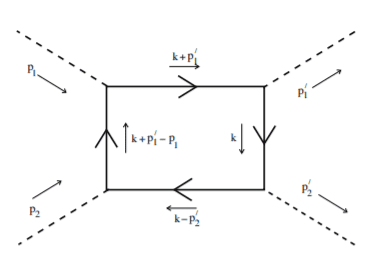I have no guess for what we would get out of $\left(\frac{i\lambda_4}{4!}\right)^2\frac{1}{2!} \int d^4 x d^4 y \langle f| T\left\{ : \phi (x)\phi (x)\phi (x)\phi (x) :: \phi (y)\phi (y)\phi (y)\phi (y) \right\}: |i\rangle$

So I would say that the Feynman rules basically stay the same except for the interaction vertices.

So my questions are:

Is there an alternative approach to derive the Feynman Rules for such a theory (which avoids the evaluation of the S-matrix)?

Do you agree with my guess?

Thank you

 

[eljose79]

Thank you for your interesting post. I would like to offer my perspective on your questions.

Firstly, let me address your first question about alternative approaches to deriving the Feynman rules for weakly coupled theories. One possible approach is to use the path integral formalism, which allows us to write the S-matrix as a functional integral over all possible field configurations. This approach can be more efficient and intuitive in certain cases, and may be worth exploring for your specific theory.

Secondly, I would like to comment on your guess for the Feynman rules. Your intuition about the interaction vertices is correct. As you mentioned, the left diagram corresponds to the first term in the S-matrix expansion, while the right diagram corresponds to the second term. For the third and fourth terms, you can expect to get similar diagrams with more interaction vertices, corresponding to higher-order terms in the S-matrix expansion. These Feynman diagrams will involve more external legs and interaction vertices, but the basic structure will remain the same.

Thank you for sharing your thoughts and questions with the forum. I hope my response has been helpful and I wish you all the best in your research.