chris25
- 6
- 0
- Homework Statement
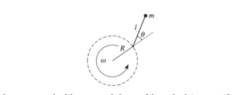
- A pendulum is designed for use on a gravity-free spacecraft. The pendulum consists of a mass at the end of a rod of length l. The pivot at the other end of the rod is forced to move in a circle of radius R with angular frequency ω. Let θ be the angle the rod makes with the radial direction. Show this system behaves exactly like a pendulum of length l in a uniform gravitational field g = ω𝑅^2. That is, show that θ(t) is a solution for one system if and only if it is for the other.
- Relevant Equations
- F=wR^2
I was confused by how to work this problem in a rotating frame. The solution read that the centrifugal force on the mass should be of magnitude 𝑚𝑤𝑅^2. However, I thought it would be 𝑚𝑤𝐿^2 where L is the distance between the mass and the center of the circle (L = l + R). What am I missing here?