Field (Bz) Inside Axially Magnetized Permanent Ring Magnet

[Helmholtzerton]

Hello,

I'm trying to find an equation which describes B(z) inside of a permanent ring magnet that is axially magnetized. Also, depending on if the equation holds true, if the ring magnet will behave as a magnetic mirror.

Below is an equation which describes the axial field of such a magnet, however I believe the equation is only valid when considering a distance starting from the ending face of the magnet.

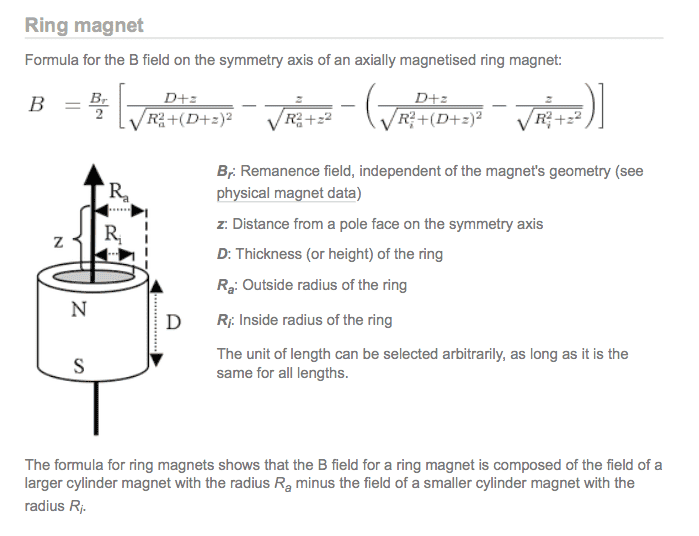
When I use this equation for a magnet with the parameters shown below, here is the field which is visualized.

Parameters:
Br 12000
Thickness 0.1 [m]
R(out) 0.18 [m]
R(in) 0.1 [m]

Its important to note that I shifted the graph below by .05 [m] to center the ring magnet at the origin.

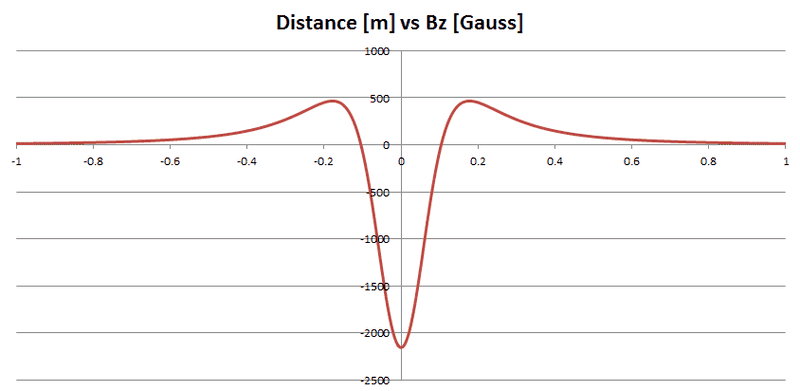I'm surprised to discover that the field inside the magnet actually flips directions. I thought perhaps the equation shown above which describes this field, was inaccurate inside the magnet. But then I found this picture.

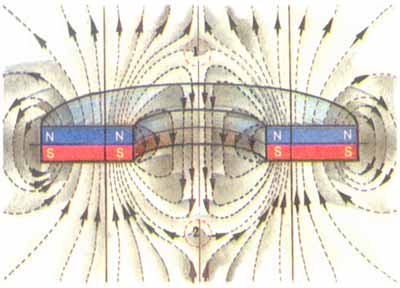
Which appears to show exactly that. I have yet to find any graphs produced by finite element analysis software which would give me more confidence in the equation for B(z) shown above.

My questions are, does anyone have experience solving the magnetic field for a ring magnet, and can confirm that indeed the equation listed above works for all space?

And considering plasmas or charged particles, when approaching the inside of the magnet where the field grows, would this serve as a magnetic mirror in some sense?

If the charged particles are not reflected from the increasing magnetic field before reaching the inside of the magnet, will they be accelerated by the abrupt change in magnetic field? Or will they be reflected as the charged particle continues towards the center of the magnet. Perhaps even trapped between the regions where the field direction abruptly changed?

 

[Charles Link]

The magnetic field as shown in the picture, going down the opening in the center of the magnet, (and opposite the direction the field would be if the hole were filled in with magnetized material), is qualitatively what would be expected from a ring magnet that is not very long. If the magnet were a very long cylinder, the field in the center would be minimal. A " magnetic surface current" modelling of the magnet is how these conclusions can be reached. (This model ignores any magnetic "poles"). The magnetic surface currents (basically moving electrical charges) in the center opening run opposite the direction that they do on the outer surface of the cylinder. The surface currents are basically like the currents of a solenoid.(comes from the formula, surface current per unit length $K_m=M \times \hat{n}/\mu_o$ where M is the magnetization (assumed uniform in the +z direction, and $\hat{n}$ is the unit vector pointing normal from the surface. A simple calculation will show these currents have the same geometry as the currents of a solenoid). For a long cylinder, it would be like one solenoid inside the other with currents in opposite directions. The result would be zero field down the center. For a much shorter cylinder /solenoids, the currents of the inner one have more effect at determining the field in the center opening. As for your formula, I'm not particularly familiar with it, but the magnetic surface currents with Biot-Savart's law would get you an answer that you could compare it with.

 

[Charles Link]

And a follow-on to the above- A "pole model" of the magnet arrives at the same result. In the pole model, the magnetic surface charge density $\sigma_m=M*\hat{n}$ (vector dot product). In this case you get the "+" magnetic charge (fictitious, but it is mathematically accurate) on top and the "-" charge on the bottom. Down the center, the magnetic pole equation, $B=\mu_o H +M$ is simply $B=\mu_o H$ because $M=0$ there. It should be readily apparent that the magnetic field $B$ (and also $H$) which points from the "+" to the "-" pole will point downward through the center. $B$ (from $H$ ) can also be computed precisely and quantitatively by this method, just as with the surface current method above. $H$ is computed just like the $E$ for electric charges, with the inverse square law, with $\epsilon_o$ replaced by $\mu_o$. Both the surface current method and the pole method should generate identical results for the magnetic field $B$. (Note: In the magnetic pole model, magnetic surface currents are not considered. Likewise, in the magnetic surface current model, magnetic poles are considered non-existent.) Additional note-in both of these models, it is a good assumption for this problem to assume uniform magnetization $M$ for the material that points in the +z direction. One other item-In the material $B$ will point along $M$, even though $H$ from the poles is in the opposite direction. In the material, the $M$ term in the equation $B=\mu_o H+M$ will in general be larger than the $\mu_o H$ term which opposes it... One additional question I have is about your graph above. Is it for z=0? It would make sense that B flips even in that plane, because the H from the + poles points away from them, and in the center opening (for z=0) the H from the + poles has zero for its z-component, and thereby, in the center opening at z=0, the B/H field will be determined completely by the "-" poles on the bottom side.

 

[Helmholtzerton]

The magnetic field as shown in the picture, going down the opening in the center of the magnet, (and opposite the direction the field would be if the hole were filled in with magnetized material), is qualitatively what would be expected from a ring magnet that is not very long. If the magnet were a very long cylinder, the field in the center would be minimal.

Minimal and opposite in direction? I believe that is also what I am seeing when I extend the cylinder with the same parameters as above, but with the thickness increased from .1 to 2.0 [m]. (Huge magnet)

Here I consider a negative value to be in the $-\hat{z}$ direction.

A " magnetic surface current" modelling of the magnet is how these conclusions can be reached. (This model ignores any magnetic "poles"). The magnetic surface currents (basically moving electrical charges) in the center opening run opposite the direction that they do on the outer surface of the cylinder. The surface currents are basically like the currents of a solenoid.

Ahh, so it appears that in fact, this formula that I am using may indeed be correct, or at least you are confirming what I am seeing with this calculation. I am slightly confused when you mention a solenoid has similar surface currents to this ring magnet, as the fields that run normal to the plane of a current loop do not change direction when considering Biot-Savart. But I think I'm incorrectly interpreting what you are saying.

(comes from the formula, surface current per unit length $K_m=M \times \hat{n}/\mu_o$ where M is the magnetization (assumed uniform in the +z direction, and $\hat{n}$ is the unit vector pointing normal from the surface. A simple calculation will show these currents have the same geometry as the currents of a solenoid).

Yes, I'm a bit confused. Forgive me. Here is what I envision when I think of the field lines both outside and inside of a solenoid.

Which seem to have a different topology than the picture shown in the original post.

For a long cylinder, it would be like one solenoid inside the other with currents in opposite directions. The result would be zero field down the center. For a much shorter cylinder /solenoids, the currents of the inner one have more effect at determining the field in the center opening. As for your formula, I'm not particularly familiar with it, but the magnetic surface currents with Biot-Savart's law would get you an answer that you could compare it with.

Ok, this is starting to make a bit more sense now, and might explain the original formula posted, as I read somewhere explaining the formula (don't have link now) stating it considers the flux of the outsize radius and subtracts the inside radius. I'm thinking of two solenoids, one inside the other where current runs opposite relative to each other.

Which is exactly what I see when using a simple model.

Sure enough that looks just like the magnet.

Well, then, now I know I can construct a uniform field two ring magnets long. But that's about it. For anything longer, I'll need to use electromagnets.

Thank you for your reply! And I'll have to dig back into my Griffiths or Zangwell and look into surface currents...although I thought magnetic fields died off as 1/R^3.

 

[Charles Link]

For the surface current model, the single ring magnet consists of two solenoids, the outer one on the outer surface and the inner one of the inner "outer" surface. The pole model is working good though, so we can address the surface current model later. If I get a chance, I will try to compute a formula for B, first for the z=0 plane as a function of r. Another not too difficult calculation would be for B on axis as a function of z. It's kind of late here in Chicago, but I'll be sure and get back on tomorrow for further discussion. One additional item though, when Biot-Savart has R^3 in the denominator, the numerator is written as $J(x') \times R$ where $R=x-x'$ (J=current density), so that it is essentially an inverse square law.

 

[Helmholtzerton]

For the surface current model, the single ring magnet consists of two solenoids, the outer one on the outer surface and the inner one of the inner "outer" surface. The pole model is working good though, so we can address the surface current model later. If I get a chance, I will try to compute a formula for B, first for the z=0 plane as a function of r. Another not too difficult calculation would be for B on axis as a function of z. It's kind of late here in Chicago, but I'll be sure and get back on tomorrow for further discussion. One additional item though, when Biot-Savart has R^3 in the denominator, the numerator is written as $J(x') \times R$ where $R=x-x'$ (J=current density), so that it is essentially an inverse square law.

I apologize, I should have been a bit more descriptive.

I meant to say, I thought magnetic fields from a permanent magnets died off as 1/R^3 rather than an electromagnet, as someone mentioned this to me. I had used Biot Savart for the last graph which should show the fields die off as an inverse square.

Just to make sure, I did a comparison where the field strength is similar at the edge of a very thin permanent magnet vs a vary thin wire where both have the same outer diameter and the permanent magnet is essentially a disk

It appears the fields die off relatively the same. However when the disk becomes more of a ring, then the field dies off much more quickly in the "near field".

If you'd like to continue discussion or check with any kind of modeling that would be great!

 

[Charles Link]

One homework problem that recently appeared on Physics Forums is quite useful for learning the basics of both the magnetic "pole" method and magnetic surface current methods. I responded in detail to the student's post-here is a "link" to the post:
https://www.physicsforums.com/threads/magnetic-field-of-a-ferromagnetic-cylinder.863066/ Working this simpler case should be useful when applying the concepts to more complex geometries. I also looked more carefully at your graphs above. I see that they are a graph of $B_z$ vs. z along the axis of symmetry. It should be easy enough to compute the Bz along the axis of symmetry to verify the formula... (editing)...And yes, I was able to verify the formula. I will need to more carefully check all of the signs for z>0, -D<z<0, and z<-D, but it does appear to be correct for all z. For the formula, $B_r =M$. I used the magnetic pole method to verify the formula, but the surface current model using concentric solenoids with opposite currents would get you the same result. ...(editing)...Incidentally, on-axis, the $B_z$ integral can be readily evaluated by either method, and the terms that arise are simply of the form $cos(\theta)$ where $\theta$ is a limiting angle. For the finite solenoid case, (magnetic surface current method), you might have seen the difference of two cosines formula in your E&M textbook.

 

[Helmholtzerton]

One homework problem that recently appeared on Physics Forums is quite useful for learning the basics of both the magnetic "pole" method and magnetic surface current methods. I responded in detail to the student's post-here is a "link" to the post:
https://www.physicsforums.com/threads/magnetic-field-of-a-ferromagnetic-cylinder.863066/ Working this simpler case should be useful when applying the concepts to more complex geometries. I also looked more carefully at your graphs above. I see that they are a graph of $B_z$ vs. z along the axis of symmetry. It should be easy enough to compute the Bz along the axis of symmetry to verify the formula... (editing)...And yes, I was able to verify the formula. I will need to more carefully check all of the signs for z>0, -D<z<0, and z<-D, but it does appear to be correct for all z. For the formula, $B_r =M$. I used the magnetic pole method to verify the formula, but the surface current model using concentric solenoids with opposite currents would get you the same result. ...(editing)...Incidentally, on-axis, the $B_z$ integral can be readily evaluated by either method, and the terms that arise are simply of the form $cos(\theta)$ where $\theta$ is a limiting angle. For the finite solenoid case, (magnetic surface current method), you might have seen the difference of two cosines formula in your E&M textbook.

Charles, thank you so much. Hilariously enough we are now covering this in my graduate E&M course (Zangwill). I talked to my professor about how I was able to model a permanent ring magnet with opposing current loops. He was like "Oh yeah, surface currents... we'll be covering that this week."

Luckly he showed me how to find off-axis field components for current loops using spherical harmonics (I found something online using elliptical integrals and it looked much harder to program in Matlab). So, I won't need that finite element analysis software just yet.

You're the best man, thanks again.

 

[Javier Lopez]

I have following troubles:
Writting at excel in cell C6 to C9: Br, D, Ro and Ri I have at any coordinate at B column I obtain at C column the field by using this formula:
=C$6*0.5*( (B12+C$7*0.5)/SQRT(C$8*C$8+(B12+C$7*0.5)*(B12+C$7*0.5))- (B12-C$7*0.5)/SQRT(C$8*C$8+(B12-C$7*0.5)*(B12-C$7*0.5)) -(B12+C$7*0.5)/SQRT(C$9*C$9+(B12+C$7*0.5)*(B12+C$7*0.5))+ (B12-C$7*0.5)/SQRT(C$9*C$9+(B12-C$7*0.5)*(B12-C$7*0.5)))
But appear to gives almost double than in the online calculators.

I made also following code, then appear to be pi multiplied by obtained data using the above formula.
I obtained the formula from: "Cylindrical Magnets and Ideal Solenoids by Norman dolby"
Here is the C++ code:

double carlson(double kc, double p, double  c, double  s);
//Sacado de: Cylindrical Magnets and Ideal Solenoids, Norman Derby
//R=radio del iman, B0=campo del iman (segun material). Z=ancho del iman axialmente, r=distancia desde el eje del iman y z=distancia desde el centro del iman axialmente
void Magnet_cylinder3(double &Br, double &Bz, double B0, double R, double Z, double r, double z)
{
    //using namespace boost::math;
    double b = Z*0.5, a = R;
    double gamma = (a - r) / (a + r);

    double z_p = z + b;
    double al_p = 1.0 / sqrt(z_p*z_p + (r + a)*(r + a));
    double be_p = z_p*al_p; al_p *= a;
    double k_p = sqrt((z_p*z_p + (a - r)*(a - r)) / (z_p*z_p + (a + r)*(a + r)));

    double z_n = z - b;
    double al_n = 1.0 / sqrt(z_n*z_n + (r + a)*(r + a));
    double be_n = z_n*al_n; al_n *= a;
    double k_n = sqrt((z_n*z_n + (a - r)*(a - r)) / (z_n*z_n + (a + r)*(a + r)));
    Br = B0*(al_p*carlson(k_p, 1, 1, -1) - al_n*carlson(k_n, 1, 1, -1));
    Bz = B0*a / (a + r)*(be_p*carlson(k_p, gamma*gamma, 1, gamma) - be_n*carlson(k_n, gamma*gamma, 1, gamma));
}

//DO y DI=diametros externo e interno del iman, B0=campo del iman (segun material). Z=ancho del iman axialmente, r=distancia desde el eje del iman y z=distancia desde el centro del iman axialmente
void Magnet_ring(double &Br, double &Bz, double B0, double DO, double DI, double Z, double r, double z)
{
    double Bro, Bzo, Bri, Bzi;
    Magnet_cylinder3(Bro, Bzo, B0, DO*0.5, Z, r, z);
    Magnet_cylinder3(Bri, Bzi, B0, DI*0.5, Z, r, z);
    Br = Bro - Bri; Bz = Bzo - Bzi;
}

double carlson(double kc, double p, double  c, double  s)
{
    if (kc == 0) return 1e299;
    double errtol = .000001;
    double k = fabs(kc);
    double pp = p;
    double cc = c;
    double ss = s;
    double em = 1.;
    if (p > 0)
    {
        pp = sqrt(p);
        ss = s / pp;
    }
    else
    {
        double f = kc*kc;
        double q = 1. - f;
        double g = 1. - pp;
        f = f - pp;
        q = q*(ss - c*pp);
        pp = sqrt(f / g);
        cc = (c - ss) / g;
        ss = -q / (g*g*pp) + cc*pp;
    }
    double f = cc;
    cc = cc + ss / pp;
    double g = k / pp;
    ss = 2 * (ss + f*g);
    pp = g + pp;
    g = em;
    em = k + em;
    double kk = k;
    while (fabs(g - k) > g*errtol)
    {
        k = 2 * sqrt(kk);
        kk = k*em;
        f = cc;
        cc = cc + ss / pp;
        g = kk / pp;
        ss = 2 * (ss + f*g);
        pp = g + pp;
        g = em;
        em = k + em;
    }
   //CHANGE (M_PI / 2.) by 0.5 or you will have wrong results!
    return (M_PI / 2.)*(ss + cc*em) / (em*(em + pp));
}

So perhaps result is ok in my excel formula and my c++ code but divided by pi[/code]

 

[Charles Link]

@Javier Lopez Your first formula looks different from the formula that the OP has presented in post 1 above. I don't know that it is incorrect, but I am led to believe that it is.

 

[Javier Lopez]

Thank you Charles, my formula calculates from center of the magnet but the formula in first post and also in the web begins at magnet border! :)

So I think that in my C++ code (that works off axis also) I should change (M_PI / 2.) by 0.5 in the carlson function.

My only doubt is if it is a good idea try first, second and third orders elliptic integral or use the carlson only that is quick and works

If somebody want use my code can make simulators, electronic microscopes, plasma thrusters, linear accelerators or magnetic fusion

 

[Helmholtzerton]

Hey, if you would like, this is how I solve for off axis fields of a current loop using elliptical integrals. This is done in python.

"""
Created on Fri Oct 26 13:52:32 2018

@author: Nate Z
"""
from pylab import *
from scipy.special import *

# Calculates Bz and Br converted back to Cartesian.
# The displayed field shows Bx and By components in a 2D plane normal current loop plane

R = .38;                 # Starting Radius of inside current loops
I = 200;                 # Current in current loop
W = 0.016129;            # Diameter of square magnet wire
columns = 7;             # number of Loops in column
rows = 7;                # number of Loops in row
u0 = 1.2566e-2;          # Permeability of free Space

LX = 1;                  # Length of solved Domain
LY = .5;                 # Width of solved Domain
NX = 100;                # Number of cells in Length
NY = 100;                # Number of cells in Width# Centers simulation
XBGN = -LX/2
XEND = LX/2;
YBGN = -LY/2;
YEND = LY/2;

# spatial domain where magnetic field components are solved
[x,y] = meshgrid(linspace(XBGN,XEND,NX),linspace(YBGN,YEND,NY));

# empty arrays needed for simulation domain in python
bX = ndarray(shape=(columns,rows,NX,NY),dtype=float,order='F')*0
bY = ndarray(shape=(columns,rows,NX,NY),dtype=float,order='F')*0rho = abs(y)       # Converts Y to rho for cylindrical coordinates
c1 = I*u0/(2*pi)   # Constant needed for solve

for column in range(0,columns):
    for row in range(0,rows):

        xs = x - W*row + (rows-1)*W/2   # Centers coil and changes axial position of each current Loop
        Rs = R + W*column               # Changes diameter of each current loop    

        # For use with elliptical integral
        KE = ((4*Rs*rho)/((xs**2+y**2+Rs**2)+(2*Rs*rho)))**0.5 
        [K,E] = ellipk(KE),ellipe(KE)
 
        for xL in range(0,NX):
            for yL in range(0,NY):

                # Constants needed for solve
                c2 = (xs[xL,yL]**2+(Rs+rho[xL,yL])**2)**0.5;
                c3 = K[xL,yL]+E[xL,yL]*(Rs**2-rho[xL,yL]**2-xs[xL,yL]**2)/((Rs-rho[xL,yL])**2+xs[xL,yL]**2)
                c4 = K[xL,yL]-E[xL,yL]*(Rs**2+rho[xL,yL]**2+xs[xL,yL]**2)/((Rs-rho[xL,yL])**2+xs[xL,yL]**2)
 
                bX[column,row,xL,yL] = c1/c2*c3
             
                if y[xL,0] < 0:
                    bY[column,row,xL,yL] = -xs[xL,yL]*c1/c2*c4
             
                else:
                    bY[column,row,xL,yL] = xs[xL,yL]*c1/c2*c4
     
# sum all contributions from each Loop that makes up the solenoid
bX2D = sum(sum(bX,axis=0),axis=0)
bY2D = sum(sum(bY,axis=0),axis=0)

contourf(x,y,bX2D[:,:],100)