- #1
milkism
- 118
- 15
- Homework Statement
- Transformation rules fot the fields in a lorentz boost in the z-direction.
- Relevant Equations
- Look at attempt at a solution.
Question:
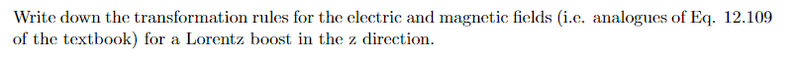
Eq. 12.109:
My solution:
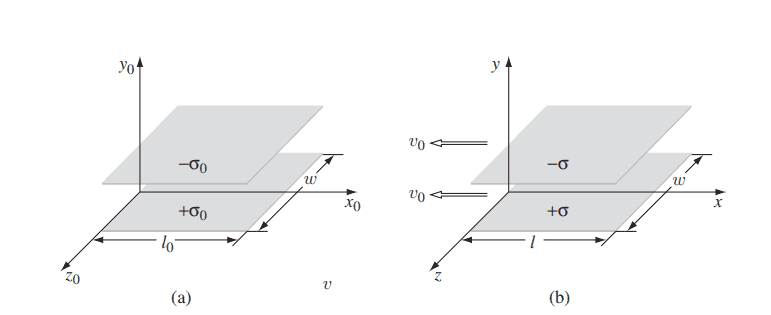
We’ll first use the configuration from figure 12.35 in the book Griffiths. Where the only difference is
that v_0 is in the z-direction. The electric field in the y-direction will be the same.
$$E_y = \frac{\sigma}{\epsilon _0}$$
Now we're going to derive the general rule, following just like how it's done in the book Griffiths. The surface current will look like:
$$\mathbf{K_{\pm}}=\mp \sigma v_0 \hat{\mathbf{z}}$$
By the right-hand rule the field would point in the positive x direction, with the magnitude as:
$$B_x = \mu_0 \sigma v_0.$$
The third system $\overline{S}$, would ofcourse travel in the z direction instead of the x direction.
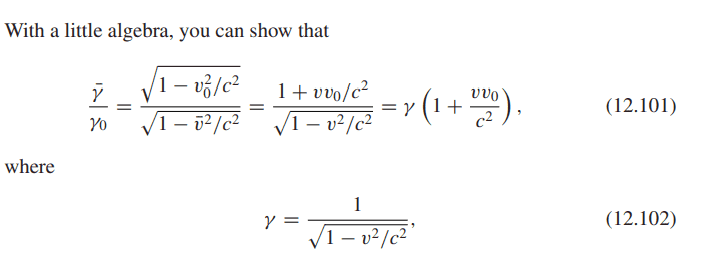
The fields will look like:
$$ \overline{E_y} = \frac{\overline{\sigma}}{\epsilon _0}$$
$$\overline{B_x} = \mu_0 \overline{\sigma} \overline{v_0}$$
Now we just need to express $\overline{\mathbf{E}}$ and $\overline{\mathbf{B}}$ in terms of $\mathbf{E}$ and $\mathbf{B}$.
We will use the same equations 12.98, 12.99, 12.101 and 12.102 to do the algebra because they didn't change.
$$\overline{E_y} = \gamma \left( E_y + vB_x \right)$$
$$\overline{B_x} = \gamma \left( B_x + \frac{v}{c^2}E_y \right)$$
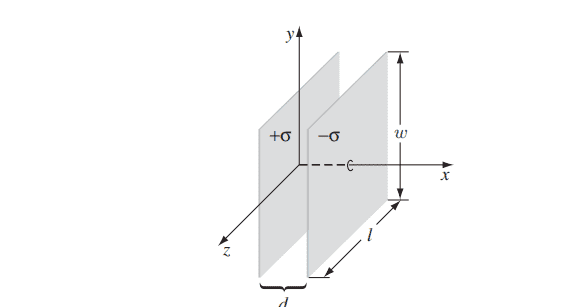
To find $E_x$ and $B_y$, the configuration will be identical to figure 12.36.
The fields in $S$ will be as follows:
$$E_x = \frac{\sigma}{\epsilon_0}$$
$$B_y = \sigma \mu_0 v_0$$
The fields in $\overline{S}$ will look like:
$$\overline{E_x} = \gamma \left( E_x + vB_y \right)$$
$$\overline{B_y} = \gamma \left( B_y + \frac{v}{c^2}E_x \right)$$
For the z component of the electric fields will be same and for the magnetic will also be the same, if we take a solenoid parallel to the z-axis.
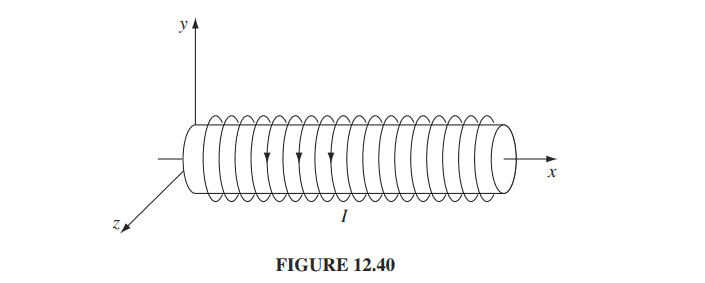But the solenoid being on the z-axis.
$$\overline{B_z} = B_z$$
$$\overline{E_z} = E_z$$
I'm not exactly sure if I'm right, because it all depends if your configuration is correct.
Eq. 12.109:
My solution:
We’ll first use the configuration from figure 12.35 in the book Griffiths. Where the only difference is
that v_0 is in the z-direction. The electric field in the y-direction will be the same.
$$E_y = \frac{\sigma}{\epsilon _0}$$
Now we're going to derive the general rule, following just like how it's done in the book Griffiths. The surface current will look like:
$$\mathbf{K_{\pm}}=\mp \sigma v_0 \hat{\mathbf{z}}$$
By the right-hand rule the field would point in the positive x direction, with the magnitude as:
$$B_x = \mu_0 \sigma v_0.$$
The third system $\overline{S}$, would ofcourse travel in the z direction instead of the x direction.
The fields will look like:
$$ \overline{E_y} = \frac{\overline{\sigma}}{\epsilon _0}$$
$$\overline{B_x} = \mu_0 \overline{\sigma} \overline{v_0}$$
Now we just need to express $\overline{\mathbf{E}}$ and $\overline{\mathbf{B}}$ in terms of $\mathbf{E}$ and $\mathbf{B}$.
We will use the same equations 12.98, 12.99, 12.101 and 12.102 to do the algebra because they didn't change.
$$\overline{E_y} = \gamma \left( E_y + vB_x \right)$$
$$\overline{B_x} = \gamma \left( B_x + \frac{v}{c^2}E_y \right)$$
To find $E_x$ and $B_y$, the configuration will be identical to figure 12.36.
The fields in $S$ will be as follows:
$$E_x = \frac{\sigma}{\epsilon_0}$$
$$B_y = \sigma \mu_0 v_0$$
The fields in $\overline{S}$ will look like:
$$\overline{E_x} = \gamma \left( E_x + vB_y \right)$$
$$\overline{B_y} = \gamma \left( B_y + \frac{v}{c^2}E_x \right)$$
For the z component of the electric fields will be same and for the magnetic will also be the same, if we take a solenoid parallel to the z-axis.
$$\overline{B_z} = B_z$$
$$\overline{E_z} = E_z$$
I'm not exactly sure if I'm right, because it all depends if your configuration is correct.
.
