Fields and Field Extensions - Lovett, Chapter 7 .... ....

[Math Amateur]

I am reading Abstract Algebra: Structures and Applications" by Stephen Lovett ...

I am currently focused on Chapter 7: Field Extensions ... ...

I need help with the proof of, or at least some remarks concerning Example 7.1.5 ...Example 7.1.5 reads as follows:

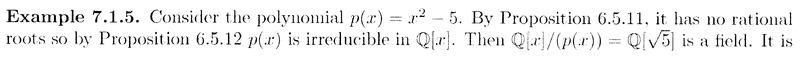
In the above text from Lovett, we read the following:

" ... ... Then $\mathbb{Q} [x] / ( p(x) ) = \mathbb{Q} [ \sqrt{5} ]$ is a field. ... ... "
I understand that $\mathbb{Q} [x] / ( p(x) ) = \mathbb{Q} [x] / ( x^2 - 5 )$ is a field ... ... but why is it equal to $\mathbb{Q} [ \sqrt{5} ]$ ... ... ?Can someone please explain and demonstrate why the equality $\mathbb{Q} [x] / ( x^2 - 5 ) = \mathbb{Q} [ \sqrt{5} ]$ holds ... ?Help will be appreciated ...

Peter

 

[andrewkirk]

I think perhaps he means to indicate the two rings are isomorphic rather than equal. Set-theoretically they are distinct objects.

The function $\psi:\mathbb Q[\sqrt 5]\to \mathbb Q[x]/(p(x))$ given by $\psi(a+b\sqrt 5) = (a+bx)+(p(x))$ looks promising to me as a potential isomorphism.

 

[Math Amateur]

Hi Andrew,

Thanks for the help ...

Just reflecting on what you have written...

Peter

 

[fresh_42]

I understand that $\mathbb{Q} [x] / ( p(x) ) = \mathbb{Q} [x] / ( x^2 - 5 )$ is a field ... ... but why is it equal to $\mathbb{Q} [ \sqrt{5} ]$ ... ... ?

It is the same as with another more famous field. Nobody writes $\mathbb{F} := \mathbb{R}[x]/ (x^2+1)$ in daily life. But everybody is used to the roots of $x^2+1$ which we call $\pm i$ and write $\mathbb{F} = \mathbb{R} [ i ] = \mathbb{C}$. And we can also use equality signs here instead of isomorphisms because it is a canonical (maybe natural, but I haven't checked) isomorphism for it is simply the definition of $i$ or $\sqrt{5}$, namely as the root of $x^2-5$.

 

[Math Amateur]

Thanks Andrew and fresh_42 ... appreciate your help ... understanding the ideas here better ...

BUT ... still not fully at ease with the ideas ...

So ... been reading Dummit and Foote Chapter 13, Field Theory ... and in particular Theorems 3 and 4 on pages 512-514 ... (see below)

So ... interpreting Lovett Example 7.1.5 in terms of the notation and ideas of D&F Theorems 3 and 4, Chapter 13 ...

... we have ...

$p(x) = x^2 -5$ is irreducible in $\mathbb{Q} [x]$

and $K = F[x] / ( p(x) ) = F[x] / ( x^2 - 5 )$ is a field with root $\overline{x} = x \text{ mod } (x^2 - 5 )$

... BUT ...

... how do we (formally and rigorously) demonstrate that $\overline{x} = x \text{ mod } (x^2 - 5 ) = \sqrt{5}$ ... ...Since i find this difficult/awkward to do ... I feel I am not fully understanding the concepts and mechanics involved ...

Can someone please help ...

Peter
====================================================================================================

I have referred to Theorems 3 and 4 of D&F Chapter 13 ... The statement and proof of Theorem 3 plus the statement of Theorem 4 follows:

 

[fresh_42]

Consider the short exact sequence
$$\{0\} \rightarrow \mathcal{I} := \operatorname{ker} \pi \stackrel{\subseteq}{\rightarrowtail} \mathbb{Q}[x] \stackrel{\pi}{\twoheadrightarrow} \mathbb{Q}[\sqrt{5}] \rightarrow \{0\}
$$
with $\pi(f(x)) = f(\sqrt{5})$. Now $\mathbb{Q}[\sqrt{5}] \cong \mathbb{Q}[x]/\mathcal{I}$. Determine $\mathcal{I}$.

 

[Math Amateur]

Consider the short exact sequence
$$\{0\} \rightarrow \mathcal{I} := \operatorname{ker} \pi \stackrel{\subseteq}{\rightarrowtail} \mathbb{Q}[x] \stackrel{\pi}{\twoheadrightarrow} \mathbb{Q}[\sqrt{5}] \rightarrow \{0\}
$$
with $\pi(f(x)) = f(\sqrt{5})$. Now $\mathbb{Q}[\sqrt{5}] \cong \mathbb{Q}[x]/\mathcal{I}$. Determine $\mathcal{I}$.

Thanks fresh_42 ... but will have to work on this ... only have a very fleeting knowledge of exact sequences ...

Will need to revise them a bit ..

Back to you when I can ...

Peter

 

[fresh_42]

It's an isomorphism theorem, I think it's called (1st?). Having a surjective ring homomorphism $\pi : R \longrightarrow Q$, then $\pi(R) = Q \cong R / (\operatorname{ker}\pi)$. The short exact sequence above is merely another notation of it.
The point is to prove $\mathcal{I} := \operatorname{ker} \pi = \{f(x) \in \mathbb{Q}[x]\,\vert \,\pi(f(x))=f(\sqrt{5})= 0\} = \langle (x^2-5) \rangle$.

 

[Math Amateur]

Hi fresh_42 ... yes, OK ...think I am getting the hang of things ...

But ... need to be sure of mapping $\pi$ ... and the thinking that went into determining and using it ...I am assuming from the short exact sequence that $\pi$ is defined as follows:

$\pi \ : \ \mathbb{Q} [x] \longrightarrow \mathbb{Q} [ \sqrt{5} ]$ ... where $\pi (f(x) ) = f( \sqrt{5} )$

Is that right?It would help me immeasurably to know what thinking went into determining $\pi$ ...

... ... in particular, what thinking went into determining the codomain $\mathbb{Q} [ \sqrt{5} ]$ ...?If the above is correct I am somewhat lost as to how your use of $\pi$ ties up with $\pi$ in D&F Proposition 2 ( see previous post)Hope you can help ...

Peter

 

[fresh_42]

I am assuming from the short exact sequence that $\pi$ is defined as follows:

$\pi \ : \ \mathbb{Q} [x] \longrightarrow \mathbb{Q} [ \sqrt{5} ]$ ... where $\pi (f(x) ) = f( \sqrt{5} )$

Is that right?

Yes.

It would help me immeasurably to know what thinking went into determining $\pi$ ...

... ... in particular, what thinking went into determining the codomain $\mathbb{Q} [ \sqrt{5} ]$ ...?

That's what we do: $a=\pm \sqrt{5} \Leftrightarrow a^2-5=p(a)=0 \Leftrightarrow p(\pm \sqrt{5})=0$, i.e. it's kind of natural to consider the evaluation of polynomials at $\pm \sqrt{5}$. Of course both signs could be equally used here. The evaluation of polynomials at a certain point $a$ is a ring homomorphism, and $p(a) \in \mathbb{Q}[\sqrt{5}]$ as well as $p(x) \in \mathbb{Q}[x]/(p(x))$ are both zero in their according rings, i.e. $\pi$ is a ring homomorphism that maps zero to zero, which is a good start to look closer at it.

In general, $\{\textrm{ polynomial ring over a field }F \}/\{\textrm{ ideal generated by an irreducible polynomial }p\}$ is a field. Which one? The zero element is clearly $\bar{p}(x)$ and the identity $\bar{1}$. So whether we plug in elements of $F$ here, or we consider Andrew's isomorphism in post #2, which does it the other way around, by substitution of $x$ by $\{\textrm{ root }\;a\;{ of }\;p\}$, doesn't matter. In the end, the definition of $a$, e.g. $a=\sqrt{5}$ is used. I mean it's only a symbol for $p(a)=0$ which is the "plug in".

If the above is correct I am somewhat lost as to how your use of $\pi$ ties up with $\pi$ in D&F Proposition 2 ( see previous post)Hope you can help ...

Peter

Well, I already knew $F[x]/(p(x))\cong^{(*)} F[a]$ which makes it a bit easier. One considers $F[x] \twoheadrightarrow F[x]/(p(x))$ or one considers $F[x] \twoheadrightarrow F[a]$. So your question is somehow: How do we know which one? The obvious answer is: Because (*) is the assertion to be proven, so it shouldn't matter. The deeper answer could involve the question: How did we know the first time? That's naturally difficult to tell, but as one are polynomials and one are polynomials with a root plugged in, it's not that far to consider $f(x) \mapsto f(a)$.

I'm not really sure whether this covers your question. The medium here is a bit limited to answer these kind of questions.

 

[andrewkirk]

... how do we (formally and rigorously) demonstrate that $\overline{x} = x \text{ mod } (x^2 - 5 ) = \sqrt{5}$ ... ...

I'll have a go at explaining it without using exact sequences.

Observe that $\overline x\triangleq \pi(x)=x+(p(x))$. Square this and writing $K\triangleq {F(x)/(p(x))}$ and $(p(x))$ for the ideal of $F[x]$ generated by $p(x)$, we get:
$$\overline x{}^2 - 5_K= (x+(p(x)))\cdot (x+(p(x))) - (5+p(x))\triangleq (x\cdot x-5) + (p(x)) = (x^2 -5)+ (p(x))=(p(x))=0_K$$
Hence $\overline x$ satisfies the equation $y_{K}{}^2-5_K=0_K$ which is the defining equation of a square root of 5 in the field $K$.

This is not a complete proof by any means, but perhaps it may help with gaining an intuition. I hope it makes sense. I"m in a bit of a rush today so didn't get time to check it.

 

[mathwonk]

suppose we consider polynomials, with real coefficients, in the number sqrt(5). or suppose we consider polynomials in X and then we set X^2 = 5 everywhere, i.e. we set X = sqrt(5). what is the difference?

 

[Math Amateur]

suppose we consider polynomials, with real coefficients, in the number sqrt(5). or suppose we consider polynomials in X and then we set X^2 = 5 everywhere, i.e. we set X = sqrt(5). what is the difference?

Thanks for the help, mathwonk ...

Well ... indeed ... it seems there is no difference ...

So ... I am taking it that you are giving an explanation of why $\mathbb{R} [ \sqrt{5}]$ is isomorphic to $\mathbb{R} [x] / (x^2 - 5)$ ...

Is that correct?

We would also have an isomorphism if we substituted $\mathbb{Q}$ for $\mathbb{R}$ ... is that correct? ( that is we have an isomorphism if we consider polynomials with rational coefficients)

Peter

 

[Math Amateur]

I'll have a go at explaining it without using exact sequences.

Observe that $\overline x\triangleq \pi(x)=x+(p(x))$. Square this and writing $K\triangleq {F(x)/(p(x))}$ and $(p(x))$ for the ideal of $F[x]$ generated by $p(x)$, we get:
$$\overline x{}^2 - 5_K= (x+(p(x)))\cdot (x+(p(x))) - (5+p(x))\triangleq (x\cdot x-5) + (p(x)) = (x^2 -5)+ (p(x))=(p(x))=0_K$$
Hence $\overline x$ satisfies the equation $y_{K}{}^2-5_K=0_K$ which is the defining equation of a square root of 5 in the field $K$.

This is not a complete proof by any means, but perhaps it may help with gaining an intuition. I hope it makes sense. I"m in a bit of a rush today so didn't get time to check it.

Thanks Andrew ...

It seems to me to make excellent sense ... indeed it is the demonstration I was looking for ... and seems rigorous ...

Peter

 

[Math Amateur]

Yes.

That's what we do: $a=\pm \sqrt{5} \Leftrightarrow a^2-5=p(a)=0 \Leftrightarrow p(\pm \sqrt{5})=0$, i.e. it's kind of natural to consider the evaluation of polynomials at $\pm \sqrt{5}$. Of course both signs could be equally used here. The evaluation of polynomials at a certain point $a$ is a ring homomorphism, and $p(a) \in \mathbb{Q}[\sqrt{5}]$ as well as $p(x) \in \mathbb{Q}[x]/(p(x))$ are both zero in their according rings, i.e. $\pi$ is a ring homomorphism that maps zero to zero, which is a good start to look closer at it.

In general, $\{\textrm{ polynomial ring over a field }F \}/\{\textrm{ ideal generated by an irreducible polynomial }p\}$ is a field. Which one? The zero element is clearly $\bar{p}(x)$ and the identity $\bar{1}$. So whether we plug in elements of $F$ here, or we consider Andrew's isomorphism in post #2, which does it the other way around, by substitution of $x$ by $\{\textrm{ root }\;a\;{ of }\;p\}$, doesn't matter. In the end, the definition of $a$, e.g. $a=\sqrt{5}$ is used. I mean it's only a symbol for $p(a)=0$ which is the "plug in".

Well, I already knew $F[x]/(p(x))\cong^{(*)} F[a]$ which makes it a bit easier. One considers $F[x] \twoheadrightarrow F[x]/(p(x))$ or one considers $F[x] \twoheadrightarrow F[a]$. So your question is somehow: How do we know which one? The obvious answer is: Because (*) is the assertion to be proven, so it shouldn't matter. The deeper answer could involve the question: How did we know the first time? That's naturally difficult to tell, but as one are polynomials and one are polynomials with a root plugged in, it's not that far to consider $f(x) \mapsto f(a)$.

I'm not really sure whether this covers your question. The medium here is a bit limited to answer these kind of questions.

Thank you fresh_42 ... your post was most helpful ...

... indeed, I am still reflecting on what you have written...

Peter

 

[fresh_42]

So ... I am taking it that you are giving an explanation of why $\mathbb{R} [ \sqrt{5}]$ is isomorphic to $\mathbb{R} [x] / (x^2 - 5)$ ...

This example is more interesting with $\mathbb{Q}$ instead of $\mathbb{R}$ as $\sqrt{5}\in \mathbb{R}$ and both, $\mathbb{R} [ \sqrt{5}]$ and $\mathbb{R} [x] / (x^2 - 5)$, are only the reals again.

The more I think about it, the more I like the grip that $\sqrt{5}$ itself isn't actually a number, but rather an abbreviation for one solution of $x^2-5=0$, the positive one. We're only more used to it, as we would be, if we, e.g. wrote $\xi_5$ instead.

$\mathbb{Q}[x]/\langle x^2-5 \rangle$ does exactly this: Take the rationals plus an additional number called $x$, and identify all expressions $x^2-5$ with zero, such that $x$ doesn't behave like $\pi$ would, without any algebraic dependencies, but behaves like $\xi_5 = \sqrt{5}$ instead, where $\xi_5^2 =5$ such that $\xi_5$ becomes $\sqrt{5}$ and $x \textrm{ (with the identification } x^2-5=0\textrm{) } \leftrightarrow \sqrt{5}$ establishes a ring (field) isomorphism.