Filling a rigid tire from a pressure regulated compressed air line

[erobz]

This thought came to me while I was trying to fill my MTB bike tire a while ago as an exercise in laziness to not "check" the tire pressure with a separate gauge! Mostly, my mind just wanders...

If I have some very large tank filled with compressed air at gauge pressure Ptank. The hose runs to an idealized PRV which regulates the pressure down to Preg and holds it constant. At the other end of the hose is connected to rigid tire of volume V−tire, and initial pressure Patm (0 gauge).

How long will it take until the pressure in the tire reaches the regulated pressure ## P_{tire} = P_{reg}?

I'm just starting with Newtons Second, and analyzing from the hose to the tire and I'm already in uncharted territory:

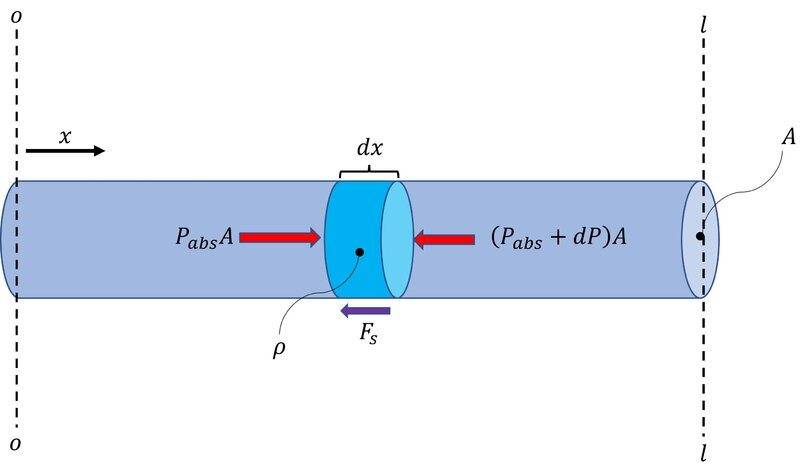
My first go was this assuming that the temperature of the flow remains constant:

$$ F_P−F_{P+dP}−F_s=A dx\frac{d}{dt} \left( \rho v \right) $$

$$ \left( P + P_{atm} \right) A - \left( P + P_{atm} + dP \right) - \tau_o \pi D dx = A dx \left( \frac{d \rho}{dt}v + \rho \frac{dv}{dt} \right) $$

Changing independent variable from time $t$ to position along the hose $x$

$$ \Downarrow $$

$$ - \frac{dP}{dx} - \frac{ \tau_o \pi D}{A} = \frac{d \rho}{dx}v^2 + \rho \frac{d}{dx} \left( \frac{v^2}{2} \right) $$

The density is given from the Ideal Gas Law:

$$ \rho = \frac{P + P_{atm}}{RT} \implies \frac{d \rho}{dx} = \frac{1}{RT} \frac{dP}{dx} $$

We then have that:

$$ - \frac{dP}{dx} - \frac{ \tau_o \pi D}{A} = \frac{1}{RT} \frac{dP}{dx} v^2 + \frac{P + P_{atm}}{RT} \frac{d}{dx} \left( \frac{v^2}{2} \right) $$

Before I go any further, am I going in the right direction?

 

[Baluncore]

Before I go any further, am I going in the right direction?

Tire pressure will never quite reach the regulated pressure, so you must leave it connected to the regulator forever.
How do you know what pressure drop there will be across the tire valve?

 

[erobz]

Tire pressure will never quite reach the regulated pressure, so you must leave it connected to the regulator forever

I would like to prove this under some reasonable assumptions (what they might be I'm not even sure), using the equation above. (or the proper equation for that matter)

How do you know what pressure drop there will be across the tire valve?

I'm ignoring the valve for the time being. The model doesn't explicitly need one. There will be a pressure drop from the flow through the hose. That pressure drop will be from $P_{reg} \to P_{tire}$ across the length of the hose as a necessity of continuity.

 

[erobz]

Tire pressure will never quite reach the regulated pressure, so you must leave it connected to the regulator forever.

However, as motivation for needing to "prove" this statement you've given should be driven by what happens if we connect two tanks by a pipe in an incompressible viscous flow.You can more simply show that the time the tanks reach equilibrium is definitely finite. So, if there is something special about compressible flows that alters this outcome I would like to try and show it.

 

[bob012345]

Tire pressure will never quite reach the regulated pressure, so you must leave it connected to the regulator forever.

Do you mean like a capacitor never gets fully charged?

 

[Baluncore]

Do you mean like a capacitor never gets fully charged?

In the equivalent RC network, yes.

Where the flow rate is proportional to the pressure difference, the flow must approach zero at an exponentially decaying rate. The time constant can be computed, or you can compute the "time to half pressure", but a perfect equality is never possible.

It is possible, with a largely unrestricted airflow, for air mass momentum to overshoot equality. It is also possible for the air to cool as it is transferred, before later warming to satisfy or exceed pressure equality.

Thermal diffusion of air molecules will at some time drive it beyond equilibrium in a random walk.

 

[bob012345]

0

Tire pressure will never quite reach the regulated pressure, so you must leave it connected to the regulator forever.

You must be at Zeno's gas station.

 

[erobz]

Are you saying without a doubt that equilibrium will never be reached in finite time for the case of a compressible flow? Is your stance based on a particular solution to the Navier-Stokes Equations, or your analogy (intuition)?

 

[erobz]

@Chestermiller

I don't mean to call you out (and understand if you are busy and don't want to sus it out). It seems like you have expertise in this arena?

 

[Baluncore]

Are you saying without a doubt that equilibrium will never be reached in finite time for the case of a compressible flow? Is your stance based on a particular solution to the Navier-Stokes Equations, or your analogy (intuition)?

Doing the math before you understand the implications of the physical model, puts you in a position where you cannot see the forest because of the trees. I do not want to get lost in the same forest by solving the same math. Both intuition and analogy tell me that perfect equality of pressure cannot be reached in finite time.

 

[erobz]

Doing the math before you understand the implications of the physical model, puts you in a position where you cannot see the forest because of the trees. I do not want to get lost in the same forest by solving the same math. Both intuition and analogy tell me that perfect equality of pressure cannot be reached in finite time.

Well, does your intuition (analogy) change if the fluid is taken to incompressible? If so, in what way?

 

[bob012345]

Are you saying without a doubt that equilibrium will never be reached in finite time for the case of a compressible flow? Is your stance based on a particular solution to the Navier-Stokes Equations, or your analogy (intuition)?

While in a purely mathematical system equilibrium will never be reached, if we consider a real system and what the time constant is then a practical state of equilibrium will be reached when the number of time constants passed is such that you have reached down a few molecules of difference which if a time constant were ~0.1 sec would be less than 1 minute.

 

[erobz]

While in a purely mathematical system equilibrium will never be reached, if we consider a real system and what the time constant is then a practical state of equilibrium will be reached when the number of time constants passed is such that you have reached down a few molecules of difference which if a time constant were ~0.1 sec would be less than 1 minute.

I get that. Practically, there will be an equilibrium. That is not exactly what I'm asking though.

 

[erobz]

Doing the math before you understand the implications of the physical model, puts you in a position where you cannot see the forest because of the trees. I do not want to get lost in the same forest by solving the same math. Both intuition and analogy tell me that perfect equality of pressure cannot be reached in finite time.

I'm just hoping to understand where certain models with implicit assumptions perhaps like "incompressible" break down, while practicing finding my way through the forest. I'm not trying to get lost in the forest, but if I do... I'd like to possesses the skills to survive until I find my way out!

 

[erobz]

I would like to try and cast some doubt by showing that for viscous, incompressible flow between two tanks, equilibrium is archived in a finite amount of time.

For incompressible viscous flow between two points 1 & 2 we have the following result derived from Conservation of Energy applied to Reynolds Transport Theorem:

$$ \frac{P_1}{\gamma} + z + \frac{v_1^2}{2g} = \frac{P_2}{\gamma} + h + \frac{v_2^2}{2g} + \sum_{1 \to 2 } h_L \tag{1} $$

For the system above we have that:

$v_1 = \dot z$

$v_2 = \dot h$

$P_1 = P_2 = 0 \rm{gauge}$

$\sum_{1 \to 2 } h_L = k \frac{v_p^2}{2g}$

Plugging that into (1):

$$ z + \frac{ \dot z^2}{2g} = h + \frac{ \dot h^2}{2g} + k \frac{v_p^2}{2g} \tag{2}$$

Next, put everything in (2) in terms of $h$ the height of the liquid surface in tank 2

Since the flow is incompressible the total volume of the system must be preserved:

$$ A_1 z + A_2 h + {V\llap{-}}_p = V\llap{-} \implies z = \frac{1}{A_1} \left( V\llap{-} - {V\llap{-}}_p - A_2 h \right) \tag{3} $$

Furthermore, by taking the derivative of (3) with respect to time $t$:

$$ \dot z = - \frac{A_2}{A_1} \dot h \tag{4} $$

By continuity we also have that:

$$ A_p v_p = A_2 \dot h \implies v_p = \frac{A_2}{A_p} \dot h \tag{5} $$

Substituting back into (2):

$$ \frac{1}{A_1} \left( V\llap{-} - {V\llap{-}}_p - A_2 h \right) + \left( \frac{A_2}{A_1} \right)^2 \frac{ \dot h^2}{2g} = h + \frac{ \dot h^2}{2g} + k \left( \frac{A_2}{A_p} \right)^2 \frac{\dot h^2}{2g} \tag{6} $$

Rearranging (6) and combining constants we end up with a first order ODE of the form:

$$ \dot h = \beta \sqrt{ \lambda - \varphi h } \tag{7}$$

Where:

$\beta = \sqrt{ \frac{2g}{ 1 + k \left( \frac{A_2}{A_p} \right)^2 - \left( \frac{A_2}{A_1} \right)^2 } }$

$\lambda = \frac{1}{A_1} \left( V\llap{-} - {V\llap{-}}_p \right)$

and

$\varphi = 1 + \frac{A_2}{A_1}$

Now, the steady state height of fluid in tank 2 can be found by setting eq (7) $\dot h = 0$

$$ h_{ss} = \frac{\lambda}{ \varphi} $$

From (3) it follows that:

$$ z = \lambda - \left( 1 - \varphi \right)h $$

$$ z_{ss} = \lambda - \left( 1 - \varphi \right) \frac{\lambda}{ \varphi} = \frac{\lambda}{ \varphi} \implies z_{ss} = h_{ss} $$

Now, all that is left to do is show that equilibrium must be reached in a finite time by solving (7) by method of separation of variables:


$$ \int \frac{dh}{ \sqrt{ \lambda - \varphi h } } = \beta \int dt $$

Performing the integration:

$$ - \frac{2}{\varphi} \left( \sqrt{ \lambda - \varphi h} - \sqrt{ \lambda - \varphi h_o} \right) = \beta t \tag{8} $$

If we substitute $h = h_{ss} = \frac{\lambda}{ \varphi}$ into (8) we are left with:

$$ t = \frac{2}{ \varphi \beta} \sqrt{ \lambda - \varphi h_o} \tag{9} $$

From this analysis it is apparent that the heights of the fluid in each tank are equivalent after a finite amount of time has passed.

Now, what ( if anything) about compressible flow destroys the "finite" result?

 

[Baluncore]

Now, what ( if anything) about compressible flow destroys this result?

While I cannot point to it, I feel there is a problem with your analysis that arises when z = h.
That is the case for both compressible flow, and incompressible flow.

The pressure difference in the viscous fluid is dropped along the thin tube. If the flow velocity is a function of that difference in pressure, or height, then the solution for dp or dh must be a decaying exponential. You appear to be asking about a very special case, when that decaying exponential finally reaches zero, which is why I keep saying, never.
z - h = e^-t ;
ln( z - h ) = -t ;
For z = h ;
t = - ln( zero ) ;
∴ t = +∞ .

 

[erobz]

While I cannot point to it, I feel there is a problem with your analysis that arises when z = h.
That is the case for both compressible flow, and incompressible flow.

The pressure difference in the viscous fluid is dropped along the thin tube. If the flow velocity is a function of that difference in pressure, or height, then the solution for dp or dh must be a decaying exponential. You appear to be asking about a very special case, when that decaying exponential finally reaches zero, which is why I keep saying, never.
z - h = e^-t ;
ln( z - h ) = -t ;
For z = h ;
t = - ln( zero ) ;
∴ t = +∞ .

Well, as far as I can tell what I have provided from (1) onward is pretty standard analysis. What that says to me is that you suspect (1) is not giving an accurate representation of reality, or perhaps I've misapplied it?

(1) is a simplification of the following:

$$ \dot Q - \dot W_s = \frac{d}{dt}\int_{cv} \left( \frac{V^2}{2} + gz + u \right) \rho \, dV\llap{-} + \int_{cs} \left( \frac{V^2}{2} + gz + h \right) \rho \, \boldsymbol V \cdot d \boldsymbol A $$

I'm going to have to look more carefully at the textbook derivation to track down all the assumptions in going from that to (1). Its certainly possible I'm incorrectly applying it.

 

[bob012345]

While I cannot point to it, I feel there is a problem with your analysis that arises when z = h.
That is the case for both compressible flow, and incompressible flow.

The pressure difference in the viscous fluid is dropped along the thin tube. If the flow velocity is a function of that difference in pressure, or height, then the solution for dp or dh must be a decaying exponential. You appear to be asking about a very special case, when that decaying exponential finally reaches zero, which is why I keep saying, never.
z - h = e^-t ;
ln( z - h ) = -t ;
For z = h ;
t = - ln( zero ) ;
∴ t = +∞ .

There could be a damped oscillation of the water level between the two tanks not necessarily a single decaying exponential.

 

[Baluncore]

There could be a damped oscillation of the water level between the two tanks not necessarily a single decaying exponential.

That is true.
For a more dense, less viscous fluid, through a larger diameter, short pipe, the momentum of the flow may result in an oscillation. But that oscillation will still be inside a decaying exponential envelope.

There are three possible modes, damped, critically damped, or oscillating. The first occasion, at which z = h occurs, is at a different time in each of those scenarios. The probability that it will be perfectly critically damped will be close to zero.

Still, we should expect to see two distinct solutions to those equations.

 

[erobz]

$$ \dot Q - \dot W_s = \frac{d}{dt}\int_{cv} \left( \frac{V^2}{2} + gz + u \right) \rho \, dV\llap{-} + \int_{cs} \left( \frac{V^2}{2} + gz + h \right) \rho \, \boldsymbol V \cdot d \boldsymbol A \tag{10} $$

Ok, I think I've figured out something. The flow is not steady (it varies in time) ,and that was a simplifying assumption of (10) that leads to (1).

Taking the straight section of pipe joining the tanks as the control volume:

$\dot Q = 0$ Net rate of heat transfer entering

$\dot W_s = 0$ Shaft work

$$ 0= \frac{d}{dt}\int_{cv} \left( \frac{V^2}{2} + gz + u \right) \rho \, dV\llap{-} + \int_{cs} \left( \frac{V^2}{2} + gz + h \right) \rho \, \boldsymbol V \cdot d \boldsymbol A $$

So examining the first term on the left, I realized this is where I went wrong:

$$ \frac{d}{dt}\int_{cv} \left( \frac{V^2}{2} + gz + u \right) \rho \, dV\llap{-}$$

The flow is assumed incompressible, there is no change in elevation and the internal energy I'm not quite sure how to precisely handle at the moment. Its going to be a function of the temperature gradient ( which I expect to be small for the tanks problem) so I'm assuming that whatever it is, its rate of change in time is very small and can be neglected.

$$ \frac{d}{dt}\int_{cv} \left( \frac{V^2}{2} \right) \rho \, dV\llap{-} + \cancel{ \frac{d}{dt}\int_{cv} \left( gz \right) \rho \, dV\llap{-} } + \cancel{ \frac{d}{dt}\int_{cv} \left( u \right) \rho \, dV\llap{-} } = \frac{d}{dt}\int_{cv} \left( \frac{V^2}{2} \right) \rho \, dV\llap{-}$$

With incompressible flow $V^2$ can come outside of the integral, and the term reduces to:

$$ \frac{d}{dt}\int_{cv} \left( \frac{V^2}{2} \right) \rho \, dV\llap{-} = \rho { V\llap{-} }_{cv} \frac{d}{dt} \left( \frac{V^2}{2}\right) $$

For the second term in (10), nothing really changes:

The properties are assumed to be uniformly distributed across the control surfaces ( subscripts o and i refer to the outlet and inlet ) and we have that:

$$ \int_{cs} \left( \frac{V^2}{2} + gz + h \right) \rho \, \boldsymbol V \cdot d \boldsymbol A = \dot m \left[ \left( \frac{V_o^2}{2} + gz_o + h_o \right) - \left( \frac{V_i^2}{2} + gz_i + h_i \right) \right] $$

with no change in elevation, or cross sectional area of the pipe:

$$ \int_{cs} \left( \frac{V^2}{2} + gz + h \right) \rho \, \boldsymbol V \cdot d \boldsymbol A = \dot m \left( h_o - h_i \right) $$

So I believe I am left with the ODE:

$$ \begin{eqnarray} m_{cv} \frac{d}{dt} \left( \frac{V^2}{2}\right) &= \dot m \left( h_o - h_i \right) \tag*{} \\ \quad \tag{11} \\ m_{cv} V \frac{dV}{dt} &= -\rho A V \left( h_o - h_i \right) \tag*{} \end{eqnarray} $$

And I think its by the Second Law ( viscous flow ) that the quantity $h_o - h_i > 0$ and we say that its change it is proportional to $\frac{V^2}{2g}$

So that leaves me with:

$$ \frac{dV}{dt} = -\alpha V^2 \tag{12} $$

Where $\alpha$ is just a constant

This has the solution:

$$ t = \frac{1}{\alpha} \left( \frac{1}{V} - \frac{1}{V_o} \right) \tag{13} $$

and as $V \to 0$, $t \to \infty$

Is that what you had in mind for the type of solution?

At this point, tackling this for compressible flow might be over my head, I take your word on that.

 

[Chestermiller]

Is the regulated pressure such that, after the regulator, the gas can be treated as nearly ideal (say 3 bars or less)? Is the internal volume of the hose much less than the internal volume of the tire?

 

[erobz]

Is the regulated pressure such that, after the regulator, the gas can be treated as nearly ideal (say 3 bars or less)? Is the internal volume of the hose much less than the internal volume of the tire?

I would say those constraints could be made reasonably in most cases. Perhaps, the volume of the hose might not be insignificant in the case of a bicycle tire, but the pressure is likely under 3 bar, In the case of a truck tire the hose volume might be insignificant, but the (absolute) pressure might be a little over 3 Bar.

This was framed as a "real" problem, but my aim was to treat it from a theoretical perspective. "Will the tire ever reach the regulated pressure, or will it only forever approach it from below?" was my intended discussion.

 

[erobz]

I was wondering if before we get into the compressible flow ( because I don't understand incompressible flow as well as I thought yet), if you could take a look at post #20

https://www.physicsforums.com/threa...ated-compressed-air-line.1015542/post-6636488

Initially I got the problem wrong because my equation (1) in post #15 was not applicable. @Baluncore and @bob012345 thought that equilibrium should only ever be approached via oscillation, exponential decay, or some combination of both. After I looked more carefully at the equation from which (1) was derived, Eq (10) in post #20, I saw my error. (1) assumes steady flow, and the flow in the pipe connecting the two tanks is changing in time (unsteady).

So I whittled (10) down to (13) for the velocity of the flow in the pipe as a function of time, which does have the behavior that they propose that as $V \to 0, t \to \infty$ . However, in doing so I invoked what I though was a consequence of the Second Law for the change in enthalpy across the pipe as well as some other simplifying assumptions about the internal energy earlier:

$$ \begin{eqnarray} m_{cv} \frac{d}{dt} \left( \frac{V^2}{2}\right) &= \dot m \left( h_o - h_i \right) \tag*{} \\ \quad \tag{11} \\ m_{cv} V \frac{dV}{dt} &= -\rho A V \left( h_o - h_i \right) \tag*{} \end{eqnarray} $$

And I think its by the Second Law ( viscous flow ) that the quantity $h_o - h_i > 0$ and we say that its change it is proportional to $\frac{V^2}{2g}$

but I'm not sure that is legitimate?

 

[bob012345]

For the original tire problem, what exactly does the regulator do? Does it just maintain a constant pressure at its end of the hose like a boundary condition? Does it input gas from the tank to do so? If so then doesn't there have to be a source term in the differential equation?

 

[erobz]

What exactly does the regulator do? Does it just maintain a constant pressure at its end of the hose like a boundary condition? Does it input gas from the tank to do so? If so then doesn't there have to be a source term in the differential equation?

It's just an idealization of a device that regulates the pressure to be constant ( a boundary condition ), so I don't have to consider the change in pressure of the source. It doesn't need to be there, other than to describe the application, and how this system attempts to function in "real life". We could just replace it with an very large supply tank at the desired pressure.

 

[bob012345]

View attachment 302028

$$ \dot Q - \dot W_s = \frac{d}{dt}\int_{cv} \left( \frac{V^2}{2} + gz + u \right) \rho \, dV\llap{-} + \int_{cs} \left( \frac{V^2}{2} + gz + h \right) \rho \, \boldsymbol V \cdot d \boldsymbol A \tag{10} $$

Ok, I think I've figured out something. The flow is not steady (it varies in time) ,and that was a simplifying assumption of (10) that leads to (1).

Taking the straight section of pipe joining the tanks as the control volume:

$\dot Q = 0$ Net rate of heat transfer entering

$\dot W_s = 0$ Shaft work

$$ 0= \frac{d}{dt}\int_{cv} \left( \frac{V^2}{2} + gz + u \right) \rho \, dV\llap{-} + \int_{cs} \left( \frac{V^2}{2} + gz + h \right) \rho \, \boldsymbol V \cdot d \boldsymbol A $$

So examining the first term on the left, I realized this is where I went wrong:

$$ \frac{d}{dt}\int_{cv} \left( \frac{V^2}{2} + gz + u \right) \rho \, dV\llap{-}$$

The flow is assumed incompressible, there is no change in elevation and the internal energy I'm not quite sure how to precisely handle at the moment. Its going to be a function of the temperature gradient ( which I expect to be small for the tanks problem) so I'm assuming that whatever it is, its rate of change in time is very small and can be neglected.

$$ \frac{d}{dt}\int_{cv} \left( \frac{V^2}{2} \right) \rho \, dV\llap{-} + \cancel{ \frac{d}{dt}\int_{cv} \left( gz \right) \rho \, dV\llap{-} } + \cancel{ \frac{d}{dt}\int_{cv} \left( u \right) \rho \, dV\llap{-} } = \frac{d}{dt}\int_{cv} \left( \frac{V^2}{2} \right) \rho \, dV\llap{-}$$

With incompressible flow $V^2$ can come outside of the integral, and the term reduces to:

$$ \frac{d}{dt}\int_{cv} \left( \frac{V^2}{2} \right) \rho \, dV\llap{-} = \rho { V\llap{-} }_{cv} \frac{d}{dt} \left( \frac{V^2}{2}\right) $$

For the second term in (10), nothing really changes:

The properties are assumed to be uniformly distributed across the control surfaces ( subscripts o and i refer to the outlet and inlet ) and we have that:

$$ \int_{cs} \left( \frac{V^2}{2} + gz + h \right) \rho \, \boldsymbol V \cdot d \boldsymbol A = \dot m \left[ \left( \frac{V_o^2}{2} + gz_o + h_o \right) - \left( \frac{V_i^2}{2} + gz_i + h_i \right) \right] $$

with no change in elevation, or cross sectional area of the pipe:

$$ \int_{cs} \left( \frac{V^2}{2} + gz + h \right) \rho \, \boldsymbol V \cdot d \boldsymbol A = \dot m \left( h_o - h_i \right) $$

So I believe I am left with the ODE:

$$ \begin{eqnarray} m_{cv} \frac{d}{dt} \left( \frac{V^2}{2}\right) &= \dot m \left( h_o - h_i \right) \tag*{} \\ \quad \tag{11} \\ m_{cv} V \frac{dV}{dt} &= -\rho A V \left( h_o - h_i \right) \tag*{} \end{eqnarray} $$

And I think its by the Second Law ( viscous flow ) that the quantity $h_o - h_i > 0$ and we say that its change it is proportional to $\frac{V^2}{2g}$

So that leaves me with:

$$ \frac{dV}{dt} = -\alpha V^2 $$

Where $\alpha$ is just a constant

This has the solution:

$$ t = \frac{1}{\alpha} \left( \frac{1}{V} - \frac{1}{V_o} \right) $$

and as $V \to 0$, $t \to \infty$

Is that what you had in mind for the type of solution?

At this point, tackling this for compressible flow might be over my head, I take your word on that.

I'm not sure what you are doing here but for the idealized problem it seems unnecessarily complicated. If you define the variable of interest as the difference in height $\rho = z - h$ of the tanks you should be able to show from simple physics that the rate of change of $\rho$ is proportional to $-\rho$.

 

[erobz]

I'm not sure what you are doing here but for the idealized problem it seems unnecessarily complicated. If you define the variable of interest as the difference in height $\rho = z - h$ of the tanks you should be able to show from simple physics that the rate of change of $\rho$ is proportional to $-\rho$.

The problem is that for some level of idealization (for instance) (10) $\to$ (1), I get a finite solution for the equilibrium time as shown in post 15. The question is what level of idealization produces the result you are after?

At its heart, (10) is the First Law of Thermodynamics repackaged for fluid systems that applies to a control volume "$cv$"bounded by a control surface "$cs$".

 

[bob012345]

The problem is that for some level of idealization (10) $\to$ (1), I get a finite solution for the equilibrium time as shown in post 15. The question is what level of idealization produces the result you are after? At its heart, (10) is the First Law of Thermodynamics repackaged for fluid systems.

If you want an idealization you should use an ideal fluid. I cannot follow what you did in post #15. I don't know where you get the last term on the RHS and what is $\gamma$. I think the Bernoulli equation in the connecting pipe would suffice here .

 

[erobz]

$\gamma = \rho g$

Divide your pink box equation through by $\gamma$ and add the viscous effects and you are at (1) in post 15

Just to put your mind at ease, I didn't derive that. That was derived by the experts wrote my Fluid Mechanics text and it is a reduction of (10) in combination with the Second Law.

I can upload that derivation from the text? But its going to lead you to the result in post 15

 

[bob012345]

γ=ρg

Divide your pink box equation through by γ and add the viscous effects and you are at (1) in post 15

Just to put your mind at ease, I didn't derive that. That was derived by the experts wrote my Fluid Mechanics text and it is a reduction of (10) in combination with the Second Law.

I can upload that derivation from the text? But its going to lead you to the result in post 15

It appears you interpreted v1=z˙ ect. so you have two fat pipes facing downward but ignore the connecting pipe. I don't know if that is valid? I suggest you ignore viscous effects for the ideal case first. Also, focus on the connecting pipe.

 

[erobz]

It appears you interpreted v1=z˙ ect. so you have two fat pipes facing downward but ignore the connecting pipe. I don't know if that is valid? I suggest you ignore viscous effects for the ideal case first. Also, focus on the connecting pipe.

I ignore the viscous effects in the tanks, because they tanks are assumed to be large, and the kinetic head is going to be very small compared the kinetic head in the pipe. Thus very small viscous losses in the tanks. The head loss in the connecting pipe is what is considered significant with $v_p$.

If you want the "Bernoulli Solution", take $k$ to be zero in post 15. The only factor that contains $k$ is $\beta$.

$\beta = \sqrt{ \frac{2g}{ 1 + k \left( \frac{A_2}{A_p} \right)^2 - \left( \frac{A_2}{A_1} \right)^2 } }$

The entire effect of the pipe disappears ( because there are none), The solution that follows remains fundamentally unchanged by ignoring viscous effects as $\beta$ is just a constant.

 

[erobz]

What I would need to know, (in the least) on whether or not (13) has issues, is whether or not the Second Law dictates that given that the net rate of heat transfer $\dot Q = 0$ the change in enthalpy is always positive in the direction of flow. That is an assumption "I thought was ok to make" to get to (13) in post #20.

 

[sonhousen]

That would be the case if the tank pressure is just high enough higher than the regulator equilibrium would take a long time if not forever but that is not what he is asking. I guess he made the assumption the tank pressure would be much higher than the regulator output pressure.

 

[erobz]

The "Energy Equation" (1) and "Bernoulli Equation" (post 28) fail because both are derived under the assumption of steady flow. The flow in the tanks problem or the filling a tire problem will not be steady, so they do not apply. Unfortunately, analyzing (10) ( the First Law of Thermodynamics) is at least a way forward (of that much I am now certain).

 

[bob012345]

See if this relates;

https://www.physics.princeton.edu/~mcdonald/examples/tirepump.pdf