Master1022
- 590
- 116
- TL;DR Summary
- The stock price follows a log-normal distribution; the linear fractional change of the stock price follows a normal distribution. What about the volatility of the stock?
Hi,
I am not sure whether this is the right forum to post this. Please let me know if I should move and will do so.
Overall question: Does the 'volatility' (i.e. standard deviation of the log returns) follow any sort of statistical distribution - maybe normal or log-normal?
Background/ Context: I was looking at some stock data from yahoo finance and was plotting out some metrics for the data. For example, I looked at a group of technology companies, calculated a metric (let us call it ##m_1##) which was the linear change in closing price from the previous day:
m_1 = \frac{c_{t} - c_{t - 1}}{c_{t-1}}
where ##c_t## is the closing price of the stock on day ##t##. The distribution came out looking something like: (Note: it will take a very long time to make/read this post if I have to post all the code and the cleaning/processing steps)
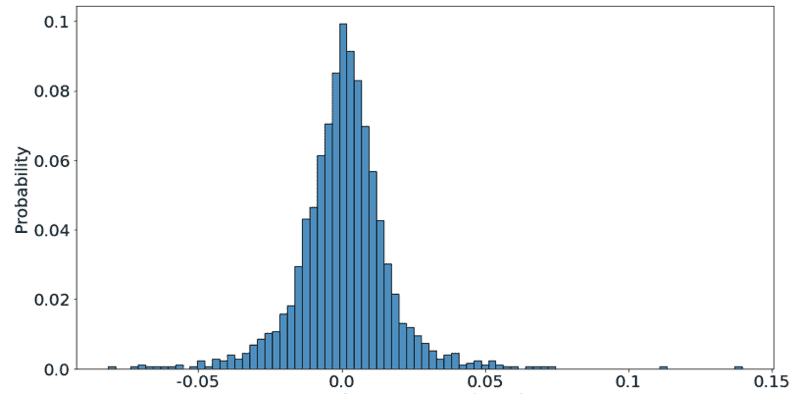
This looks somewhat fairly normal, at least from a visual standpoint. Then I thought: does that make sense that I see a normal-looking distribution?
After some searching around, it seems like yes, I do expect this value to be normally distributed. One explanation was provided on stack exchange (here) and it ends up (after some brief mathematics) by saying that stock returns are normally distributed.
From the post
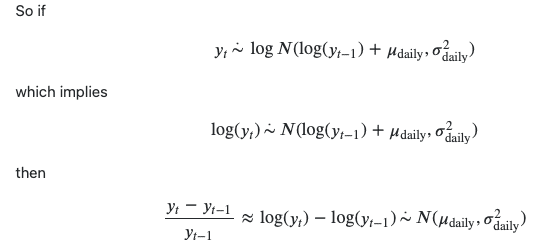
So now I am calculating the volatility using the standard deviation of the log(returns) (i.e. ## log \left( \frac{c_t}{c_{t-1}} \right) ##). Then I used a rolling window of about 10 days for the standard deviation (and also annualized it, etc. - this part doesn't matter as much in terms of the shape of the distribution as its just a scaling factor). When I plotted this out in Python, I was getting a distribution looking like this:
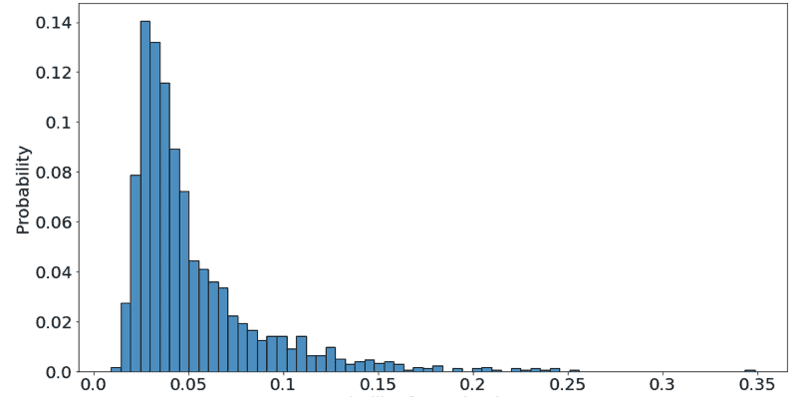
This seems lognormal to me. However, is this what we expect? I couldn't find any answers online (at least that were comprehensible by someone like me who has no stochastic/financial mathematics background). I didn't really have time to learn stochastic calculus just for this, but am just trying to understand if this aligns with expectation or not.
Any help would be greatly appreciated.
I am not sure whether this is the right forum to post this. Please let me know if I should move and will do so.
Overall question: Does the 'volatility' (i.e. standard deviation of the log returns) follow any sort of statistical distribution - maybe normal or log-normal?
Background/ Context: I was looking at some stock data from yahoo finance and was plotting out some metrics for the data. For example, I looked at a group of technology companies, calculated a metric (let us call it ##m_1##) which was the linear change in closing price from the previous day:
m_1 = \frac{c_{t} - c_{t - 1}}{c_{t-1}}
where ##c_t## is the closing price of the stock on day ##t##. The distribution came out looking something like: (Note: it will take a very long time to make/read this post if I have to post all the code and the cleaning/processing steps)
This looks somewhat fairly normal, at least from a visual standpoint. Then I thought: does that make sense that I see a normal-looking distribution?
After some searching around, it seems like yes, I do expect this value to be normally distributed. One explanation was provided on stack exchange (here) and it ends up (after some brief mathematics) by saying that stock returns are normally distributed.
From the post
So now I am calculating the volatility using the standard deviation of the log(returns) (i.e. ## log \left( \frac{c_t}{c_{t-1}} \right) ##). Then I used a rolling window of about 10 days for the standard deviation (and also annualized it, etc. - this part doesn't matter as much in terms of the shape of the distribution as its just a scaling factor). When I plotted this out in Python, I was getting a distribution looking like this:
This seems lognormal to me. However, is this what we expect? I couldn't find any answers online (at least that were comprehensible by someone like me who has no stochastic/financial mathematics background). I didn't really have time to learn stochastic calculus just for this, but am just trying to understand if this aligns with expectation or not.
Any help would be greatly appreciated.