alexmahone
- 303
- 0
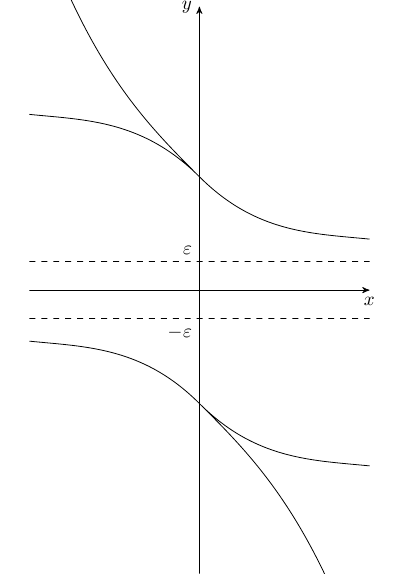
Find an $\displaystyle f(x)$ such that $\displaystyle \frac{1}{f(x)}$ is defined for all $\displaystyle x$ and is bounded, but $\displaystyle f(x)$ is decreasing.
Last edited: