anemone
Gold Member
MHB
POTW Director
- 3,851
- 115
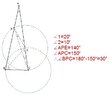
In triangle ABC, $\angle ACB=\angle ABC=80^\circ$ and $P$ is on the line segment $AB$ such that $BC=AP$. Find $\angle BPC$.