Find Area Between Circle & Function: Calc II

[MarkFL]

Here is the question:

Calculus II Find the Area between two curves and a circle with a radius of 1.?


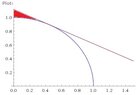
A circle with radius 1 touches the curve y = |2x| in two places(see attachment for picture). Find the area of the region that lies between the curves.

View attachment 1425

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Re: RS MASTER's question at Yahoo! Answers regading finding the area bounded by a function and circl

Hello RS MASTER,

I think what I would do, is center the circle at the origin of a new coordinate system, and then let the first quadrant line be:

\(\displaystyle y=-\frac{1}{2}x+b\) where $1\le b$

Now, we may determine the parameter $b$, by substituting for $y$ in the equation of the circle, using the linear equation, and then equate the discriminant of the resulting quadratic in $x$ to zero, since a tangent line will touch the circle in one place only, and so the resulting quadratic can only have one root. Hence:

\(\displaystyle x^2+\left(-\frac{1}{2}x+b \right)^2=1\)

Writing the quadratic in standard form, we find:

\(\displaystyle x^2+\frac{1}{4}x^2-bx+b^2=1\)

\(\displaystyle \frac{5}{4}x^2-bx+b^2-1=0\)

\(\displaystyle 5x^2-4bx+4\left(b^2-1 \right)=0\)

Equating the discriminant to zero, we find:

\(\displaystyle (-4b)^2-4(5)\left(4\left(b^2-1 \right) \right)=0\)

\(\displaystyle b^2-5\left(b^2-1 \right)=0\)

\(\displaystyle b^2=\frac{5}{4}\)

Taking the positive root, we find:

\(\displaystyle b=\frac{\sqrt{5}}{2}\)

Here is a plot of the area we will find, which we will then double to answer the given question:

View attachment 1426

Next, we need to determine the upper limit of integration, which is the $x$-coordinate of the point of tangency between the line and the circle. Thus, we need to solve:

\(\displaystyle 5x^2-2\sqrt{5}x+1=0\)

\(\displaystyle \left(\sqrt{5}x-1 \right)^2=0\)

\(\displaystyle x=\frac{1}{\sqrt{5}}\)

And so, the area $A$ we seek is given by:

\(\displaystyle A=2\int_0^{\frac{1}{\sqrt{5}}} \frac{\sqrt{5}-x}{2}-\sqrt{1-x^2}\,dx=\int_0^{\frac{1}{\sqrt{5}}} \sqrt{5}-x-2\sqrt{1-x^2}\,dx\)

At this point, it will be useful to develop a formula to handle integrals of the form:

\(\displaystyle I=\int\sqrt{a^2-x^2}\,dx\)

Let's try the trigonometric substitution:

\(\displaystyle x=a\sin(\theta)\,\therefore\,dx=a\cos(\theta)\, d\theta\)

\(\displaystyle I=a^2\int\cos^2(\theta)\,d\theta\)

Using a double-angle identity for cosine, we may write:

\(\displaystyle I=\frac{a^2}{2}\int 1+\cos(2\theta)\,d\theta\)

\(\displaystyle I=\frac{a^2}{2}\left( \theta+\frac{1}{2}\sin(2 \theta)+C \right)\)

Using the double-angle identity for sine, we have:

\(\displaystyle I=\frac{a^2}{2}\left( \theta+\sin( \theta)\cos( \theta)+C \right)\)

Back-substituting for $\theta$, we obtain:

\(\displaystyle I=\frac{a^2}{2}\left(\sin^{-1}\left(\frac{x}{a} \right)+\frac{x}{a}\cdot\frac{\sqrt{a^2-x^2}}{a}+C \right)\)

\(\displaystyle I=\frac{a^2}{2}\sin^{-1}\left(\frac{x}{a} \right)+\frac{x}{2}\sqrt{a^2-x^2}+C\)

Now, back to the integral representing the area $A$, we may now apply the FTOC as follows:

\(\displaystyle A=\left[\sqrt{5}x-\frac{1}{2}x^2-\sin^{-1}(x)-x\sqrt{1-x^2} \right]_0^{\frac{1}{\sqrt{5}}}\)

\(\displaystyle A=1-\frac{1}{10}-\sin^{-1}\left(\frac{1}{\sqrt{5}} \right)-\frac{2}{5}=\frac{1}{2}-\sin^{-1}\left(\frac{1}{\sqrt{5}} \right)\)

Now, we may check our result using some geometry. If we draw a radius of the circle from the origin to the point of tangency, we find the angle subtended by the $y$-axis and this radius is:

\(\displaystyle \alpha=\frac{\pi}{2}-\cos^{-1}\left(\frac{1}{\sqrt{5}} \right)=\sin^{-1}\left(\frac{1}{\sqrt{5}} \right)\)

Now, using the formula for the area of a triangle, and the formula for the area of a circular sector, we may write:

\(\displaystyle A=2\left(\frac{1}{2}(1)\left(\frac{\sqrt{5}}{2} \right)\sin\left(\sin^{-1}\left(\frac{1}{\sqrt{5}} \right) \right)-\frac{1}{2}(1)^2\sin^{-1}\left(\frac{1}{\sqrt{5}} \right) \right)\)

\(\displaystyle A=\frac{1}{2}-\sin^{-1}\left(\frac{1}{\sqrt{5}} \right)\)

And this checks with our result obtained from the calculus. (Sun)